题目内容
【题目】设函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)讨论函数![]() 的极值点的个数,并说明理由.
的极值点的个数,并说明理由.
【答案】(1) ![]() ;
;
(2) 综上,当![]() 时,函数有一个极值点;当
时,函数有一个极值点;当![]() 时,函数无极值点;当
时,函数无极值点;当![]() 时,函数有两个极值点
时,函数有两个极值点
【解析】
试题分析:(1)求函数的导数![]() ,则
,则![]() 时,
时,
![]()
![]() 在区间
在区间![]() 恒成立
恒成立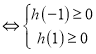 ,解此不等式组即可;
,解此不等式组即可;
(2)令![]() 则求函数
则求函数![]() 的极值点的个数
的极值点的个数![]() 求函数
求函数![]() 实根的个数,当
实根的个数,当![]() 时,函数
时,函数![]() 是常数函数,无根;当
是常数函数,无根;当![]() 时,讨论二次函数
时,讨论二次函数![]() 在区间
在区间![]() 根的情况即可.
根的情况即可.
试题解析:(1)![]() ,
,
令![]() ,要使
,要使![]() ,则使
,则使![]() 即可,而
即可,而![]() 是关于
是关于![]() 的一次函数,
的一次函数,
∴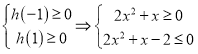 ,解得
,解得![]() 或
或![]() ,
,
所以![]() 的取值范围是
的取值范围是![]()
(2)令![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() ,函数
,函数![]() 在
在![]() 上递增,无极值点;
上递增,无极值点;
当![]() 时,
时,![]() ,
,
①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上递增,无极值点;
上递增,无极值点;
②当![]() 时,
时,![]() ,设方程
,设方程![]() 的两个根为
的两个根为![]() (不妨设
(不妨设![]() ),
),
因为![]() ,所以
,所以![]() ,由
,由![]() ,∴
,∴![]() ,
,
所以当![]() ,函数
,函数![]() 递增;
递增;
当![]() ,函数
,函数![]() 递减;
递减;
当![]() ,函数
,函数![]() 递增;因此函数有两个极值点,
递增;因此函数有两个极值点,
当![]() 时,
时,![]() ,由
,由![]() ,可得
,可得![]() ,
,
所以当![]() ,函数
,函数![]() 递增;
递增;
当![]() ,函数
,函数![]() 递减;因此函数有一个极值点,
递减;因此函数有一个极值点,
综上,当![]() 时,函数有一个极值点;
时,函数有一个极值点;
当![]() 时,函数无极值点;
时,函数无极值点;
当![]() 时,函数有两个极值点
时,函数有两个极值点

练习册系列答案
相关题目
【题目】某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取![]() 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
合计 |
|
| |
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若从第三、四、五组中用分层抽样方法抽取![]() 名学生,并在这
名学生,并在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有![]() 名学生与张老师面谈的概率.
名学生与张老师面谈的概率.