题目内容
函数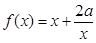 。
。
(1) 判断并证明函数的奇偶性;
(2) 若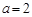 ,证明函数在(2,+
,证明函数在(2,+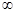 )单调增;
)单调增;
(3) 对任意的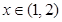 ,
,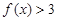 恒成立,求
恒成立,求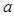 的范围。
的范围。
(1)函数为奇函数。 (2) 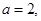 即
即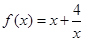 。函数在
。函数在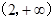 单增;(3)
单增;(3)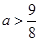 。
。
解析试题分析:(1)该函数为奇函数。…………..1分
证明:函数定义域为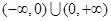
对于任意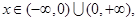 有
有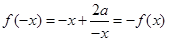
所以函数为奇函数。
(2) 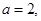 即
即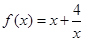 。设任意
。设任意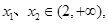 且
且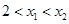
则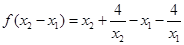
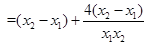
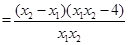
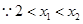
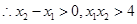 ,即
,即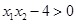
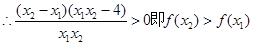
 函数在
函数在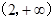 单点增
单点增
(3)由题意:对于任意 恒成立。
恒成立。
从而对于任意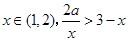 恒成立。
恒成立。
即对于任意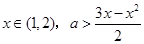 恒成立。
恒成立。
设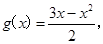 则当
则当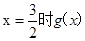 有最大值
有最大值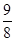 ,
,
所以,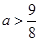 。
。
考点:本题主要考查函数的奇偶性、单调性,不等式恒成立问题。
点评:中档题,高一阶段,研究函数的奇偶性、单调性,多运用“定义”,这是处理这里问题的基本方法。对于“恒成立问题”,一般运用“分离参数法”,转化成求函数的最值问题。

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
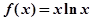 ,
,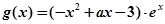 (其中
(其中 实数,
实数,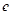 是自然对数的底数).
是自然对数的底数).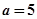 时,求函数
时,求函数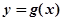 在点
在点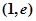 处的切线方程;
处的切线方程; 在区间
在区间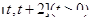 上的最小值;
上的最小值;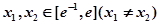 ,使方程
,使方程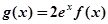 成立,求实数
成立,求实数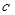 的取值范围.
的取值范围.
 的最小正周期;
的最小正周期; 对任意
对任意 ,有
,有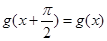 ,且当
,且当 时,
时, ;求函数
;求函数 上的解析式。
上的解析式。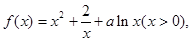
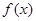 在
在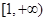 上单调递增,求
上单调递增,求 的取值范围;
的取值范围; 对于区间
对于区间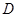 上的任意两个值
上的任意两个值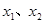 总有以下不等式
总有以下不等式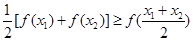 成立,则称函数
成立,则称函数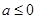 时,
时,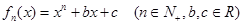
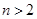 ,
,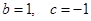 ,证明:
,证明: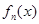 在区间
在区间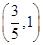 内存在唯一的零点;
内存在唯一的零点;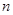 为偶数,
为偶数,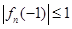 ,
,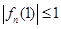 ,求
,求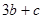 的最小值和最大值;
的最小值和最大值;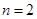 ,若对任意
,若对任意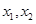
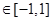 ,有
,有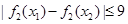 ,求
,求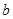 的取值范围;
的取值范围; ,
, .其中
.其中 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 .
. 的奇偶性,并说明理由;
的奇偶性,并说明理由;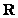 上的函数
上的函数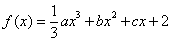 同时满足以下条件:
同时满足以下条件: 在
在 上是减函数,在
上是减函数,在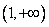 上是增函数;②
上是增函数;②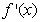 是偶函数;
是偶函数; 处的切线与直线
处的切线与直线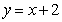 垂直.
垂直.  的解析式;
的解析式;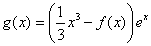 ,求函数
,求函数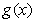 在
在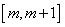 上的最小值.
上的最小值.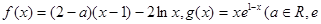 为自然对数的底数).
为自然对数的底数).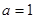 时,求
时,求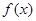 的单调区间;若函数
的单调区间;若函数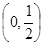 上无零点,求
上无零点,求 最小值;
最小值;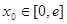 ,在
,在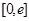 上总存在两个不同的
上总存在两个不同的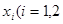 ),使
),使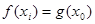 成立,求
成立,求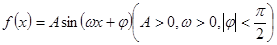 在一个周期内的部分函数图象如图所示,(I)求函数
在一个周期内的部分函数图象如图所示,(I)求函数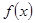 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数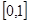 上的最大值和最小值.
上的最大值和最小值.