Question

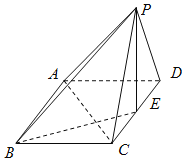
【题目】在四棱锥中，底面为矩形，平面平面，===，=2，是的中点.

（Ⅰ）求证：；

（Ⅱ）求点到平面的距离.

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）.

【解析】（Ⅰ）∵PD=PC，E为CD的中点，∴PE⊥CD，

∵平面PCD⊥平面ABCD，∴PE⊥平面ABCD，

∴PE⊥AC，（2分）

在Rt△BCE和Rt△ABC中，，∠ABC=∠BCE=90°，

∴Rt△BCE∽Rt△ABC，

∴∠BAC=∠CBE，∠ACB=∠BEC，

∴∠EBC+∠ACB=∠CAB+∠ACB=90°，

∴BE⊥CA，（5分）

∵BE∩PE=E，

∴AC平面PBE，

∴.（6分）

（Ⅱ）设点到平面的距离为，连接AE，

在Rt△EBC中，CE=1，BC=，∴BE= =，

在Rt△ADE中，AD=，DE=1，∴=，

在Rt△PEA中，PA==2， （8分）

在Rt△PEB中，PB==2，

∴=，

∵，即，解得，

∴点到平面的距离为.（12分）