题目内容
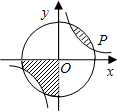 如图,点P(3a,a)是反比例函y=
如图,点P(3a,a)是反比例函y=| k |
| x |
分析:根据圆的对称性以及反比例函数的对称性可得,阴影部分的面积等于圆的面积的
,即可求得圆的半径,再根据P在反比例函数的图象上,以及在圆上,即可求得k的值.
| 1 |
| 4 |
解答:解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:
πr2=10π
解得:r=2
.
∵点P(3a,a)是反比例函y=
(k>0)与⊙O的一个交点.
∴3a2=k且
=r
∴a2=
×(2
)2=4.
∴k=3×4=12,
则反比例函数的解析式是:y=
.
故选C.
| 1 |
| 4 |
解得:r=2
| 10 |
∵点P(3a,a)是反比例函y=
| k |
| x |
∴3a2=k且
| (3a)2+a2 |
∴a2=
| 1 |
| 10 |
| 10 |
∴k=3×4=12,
则反比例函数的解析式是:y=
| 12 |
| x |
故选C.
点评:本题主要考查反比例函数图象的对称性的知识点,解决本题的关键是利用反比例函数的对称性得到阴影部分与圆之间的关系.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
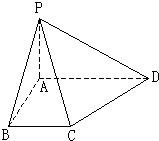 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且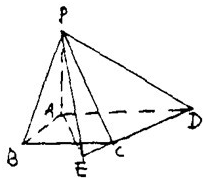 如图,梯形ABCD中,AD∥BC,∠ABC=
如图,梯形ABCD中,AD∥BC,∠ABC=
 选做题:考生在下面两小题中,任选一道作答,如果全做则按第1小题评分.
选做题:考生在下面两小题中,任选一道作答,如果全做则按第1小题评分.