题目内容
选做题：考生在下面两小题中，任选一道作答，如果全做则按第1小题评分．（1）《几何证明选讲》选做题
如图，半径分别为a和3a的圆O1与圆O2外切于T，自圆O2上一点P引圆O1的切线，切点为Q，若PQ=2a，则PT=
2
| ||
| 3 |
2
| ||
| 3 |
（2）《坐标系与参数方程》选做题
从极点O作射线交直线ρcosθ=3于点M，P为线段OM上的点，且|OM|•|OP|=12，则P点轨迹的极坐标方程为
p=4cosθ
p=4cosθ
．分析：（1）如图根据自圆O2上一点P引圆O1的切线，切点为Q，得到PQ⊥QO1，利用勾股定理得PO1的长，再在三角形PO1O2中，由余弦定理得cos∠PO1O2，最后在三角形PO1T中，再次利用余弦定理即可求出PT．
（2）设动点P的坐标为（ρ，θ），M的坐标为（ρ0，θ），则ρρ0=12，由ρ0cosθ=3，得到ρ=4cosθ即为所求；
（2）设动点P的坐标为（ρ，θ），M的坐标为（ρ0，θ），则ρρ0=12，由ρ0cosθ=3，得到ρ=4cosθ即为所求；
解答：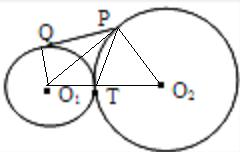
解：（1）如图，∵自圆O2上一点P引圆O1的切线，切点为Q，
∴PQ⊥QO1，
∴PO1=
=
=
a，
在三角形PO1O2中，由余弦定理得：
cos∠PO1O2=
=
，
所以在三角形PO1T中，
PT=
=
a，
故答案为：
a．
（2）设动点P的坐标为（ρ，θ），M的坐标为（ρ0，θ），
则ρρ0=12．
∵ρ0cosθ=3，
∴ρ=4cosθ，即为所求的轨迹方程．
故答案为：ρ=4cosθ．
解：（1）如图，∵自圆O2上一点P引圆O1的切线，切点为Q，∴PQ⊥QO1，
∴PO1=
PQ2+Q
|
| 4a2+a2 |
| 5 |
在三角形PO1O2中，由余弦定理得：
cos∠PO1O2=
(
| ||
2×
|
| ||
| 3 |
所以在三角形PO1T中，
PT=
(
|
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
（2）设动点P的坐标为（ρ，θ），M的坐标为（ρ0，θ），
则ρρ0=12．
∵ρ0cosθ=3，
∴ρ=4cosθ，即为所求的轨迹方程．
故答案为：ρ=4cosθ．
点评：（1）本题主要考查了圆的切线的性质、与圆有关的线段及解三角形的有关知识，属于基础题．
（2）考查简单曲线的极坐标方程和解决数学问题的能力，以及会求简单轨迹的极坐标方程．
（2）考查简单曲线的极坐标方程和解决数学问题的能力，以及会求简单轨迹的极坐标方程．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
（考生注意：请在下面两题中任选一题作答，如果都做，则按所做第1题评分）
,设直线
的参数方程是
（
为参数）。 
轴的交点是M，N为曲线C上一动点，求|MN|的最大值。
,设直线
的参数方程是
（
为参数）。 
轴的交点是M，N为曲线C上一动点，求|MN|的最大值。