Question

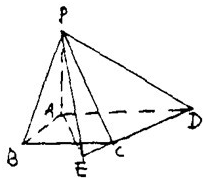如图，梯形ABCD中，AD∥BC，∠ABC=

π

2

，AB=a，AD=3a，∠ADC=arcsin

5

5

，PA⊥面ABCD，PA=a．求：
（1）二面角P-CD-A的大小（用反三角函数表示）；
（2）点A到平面PBC的距离．

Answer 1

分析：（1）作AE⊥直线CD于E连PE．由PA⊥面ABCD，根据三垂线定理知PE⊥CD．可得∠PEA是二面角P-CD-A的平面角．利用已知，分别在Rt△AED和Rt△PAE中求出即可．
（2）作AH⊥PB于H．利用线面垂直的判定与性质定理即可得出AH⊥面PBC，因此AH的长为点A到面PBC的距离．在等腰Rt△PAB中求出即可．

解答：解：（1）作AE⊥直线CD于E连PE．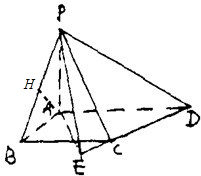
由PA⊥面ABCD据三垂线定理知PE⊥CD．∴∠PEA是二面角P-CD-A的平面角．
在Rt△AED中，AD=3a，∠ADE=arcsin

5

5

．∴AE=AD•sin∠ADE=

3 5

5

a
在Rt△PAE，中tan∠PEA=

PA

AE

=

5

3

．∴∠PEA=arctg

5

3

即二面角P-CD-A的大小为arctg

5

3

．
（2）作AH⊥PB于H．
由PA⊥面ABCD，∵BC⊥AB，∴PB⊥BC．
又PB∩AB=B，∴BC⊥面PAB．
∴BC⊥AH．
∴AH⊥面PBC，AH的长为点A到面PBC的距离．
在等腰Rt△PAB中，AH=

2

2

a．
∴点A到平面PBC的距离是

2

2

a．

点评：熟练掌握线面垂直的判定与性质定理、三垂线定理、二面角的作法、直角三角形的边角关系、点到平面的距离求法等是解题的关键．