题目内容
已知椭圆 的离心率
的离心率 ,其中一个顶点坐标为
,其中一个顶点坐标为 ,则椭圆的方程为 .
,则椭圆的方程为 .
 的离心率
的离心率 ,其中一个顶点坐标为
,其中一个顶点坐标为 ,则椭圆的方程为 .
,则椭圆的方程为 .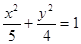
试题分析:因为顶点坐标为
 ,
, ,又由
,又由 得
得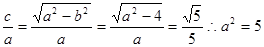 所以椭圆的方程为
所以椭圆的方程为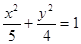
点评:主要是考查了椭圆的方程以及性质的运用,属于基础题。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
题目内容
 的离心率
的离心率 ,其中一个顶点坐标为
,其中一个顶点坐标为 ,则椭圆的方程为 .
,则椭圆的方程为 .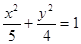
 ,
, ,又由
,又由 得
得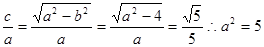 所以椭圆的方程为
所以椭圆的方程为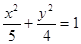

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案