题目内容
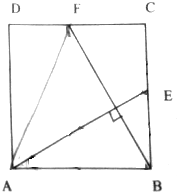
16. 如图,在四面体ABCD中,E,F分别是棱AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,已知AB=CD=3,EF=$\sqrt{5}$,求异面直线AB和CD所成的角.
如图,在四面体ABCD中,E,F分别是棱AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,已知AB=CD=3,EF=$\sqrt{5}$,求异面直线AB和CD所成的角.
分析 在BD上取靠近B的三等分点G,连接FG、GE,可证∠EGF或其补角就是异面直线AB和CD所成角,在△EFG中由勾股定理的逆定理可得∠EGF=90°,可得答案.
解答  解:(如图)在BD上取靠近B的三等分点G,连接FG、GE,
解:(如图)在BD上取靠近B的三等分点G,连接FG、GE,
在△BCD中,可得$\frac{BG}{GD}$=$\frac{BF}{FG}$,故有FG∥DC,
同理在△ABD中,可得GE∥AB,
所以∠EGF或其补角就是异面直线AB和CD所成角,
在△BCD中,由GE∥CD,CD=3,$\frac{FG}{CD}$=$\frac{1}{3}$,得FG=1,
在△ABD中,由EG∥AB,AB=3,$\frac{EG}{AB}$=$\frac{2}{3}$,得EG=2,
在△EFG中,由EG=2,FG=1,EF=$\sqrt{5}$,则EG2+FG2=EF2,
由勾股定理的逆定理,可得∠EGF=90°,
所以异面直线AB和CD所成角为90°.
点评 本题考查异面直线所成的角的求法,涉及勾股定理的逆定理的应用,属中档题.

练习册系列答案
相关题目
4.若三棱锥A-BCD中所有的棱长都相等,则二面角A-BC-D的大小的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{6}}{9}$ | D. | $\frac{2\sqrt{2}}{3}$ |
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方形,AB=PA=1,E为侧棱PA上的点,$\overrightarrow{PE}$=λ$\overrightarrow{PA}$(0<λ<1).
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方形,AB=PA=1,E为侧棱PA上的点,$\overrightarrow{PE}$=λ$\overrightarrow{PA}$(0<λ<1).