题目内容
8.如图,在正方形ABCD中,AB=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=0,则$\overrightarrow{AE}$•$\overrightarrow{AF}$=4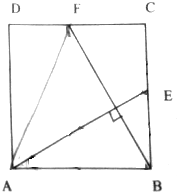
分析 F在边CD上,从而知道存在实数k,使得$\overrightarrow{CF}=k\overrightarrow{CD}$,从而根据$\overrightarrow{AE}•\overrightarrow{BF}=0$可得到$(\overrightarrow{AB}+\overrightarrow{BE})•(\overrightarrow{BC}+k\overrightarrow{CD})=0$,进行数量积的计算即可得出k=$\frac{1}{2}$,说明F为边CD中点,而$\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{DF}$,从而进行数量积的计算即可求得答案.
解答 解:根据已知条件,$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BE}$,$\overrightarrow{BF}=\overrightarrow{BC}+k\overrightarrow{CD}$,(0≤k≤1);
∴$\overrightarrow{AE}•\overrightarrow{BF}=(\overrightarrow{AB}+\overrightarrow{BE})•(\overrightarrow{BC}+k\overrightarrow{CD})=0$;
∴-k•4+2=0;
∴$k=\frac{1}{2}$;
∴F为CD中点;
∴$\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{DF}$;
∴$\overrightarrow{AE}•\overrightarrow{AF}=(\overrightarrow{AB}+\overrightarrow{BE})•(\overrightarrow{AD}+\overrightarrow{DF})$=0+2+2+0=4.
故答案为:4.
点评 考查向量加法的几何意义,共线向量基本定理,以及数量积的计算公式,相互垂直向量的数量积为0.

 如图,在四面体ABCD中,E,F分别是棱AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,已知AB=CD=3,EF=$\sqrt{5}$,求异面直线AB和CD所成的角.
如图,在四面体ABCD中,E,F分别是棱AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,已知AB=CD=3,EF=$\sqrt{5}$,求异面直线AB和CD所成的角.