题目内容
4.若三棱锥A-BCD中所有的棱长都相等,则二面角A-BC-D的大小的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{6}}{9}$ | D. | $\frac{2\sqrt{2}}{3}$ |
分析 取BC的中点E,连接AE、DE,则∠AED为二面角A-BC-D的平面角.在△ADE中利用余弦定理即得结论.
解答 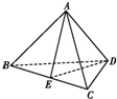 解:取BC的中点E,连接AE、DE,
解:取BC的中点E,连接AE、DE,
∵三棱锥A-BCD的棱长都相等,
∴BC⊥AE,BC⊥ED,
∴∠AED为二面角A-BC-D的平面角.
设棱长为2,则AE=$\sqrt{3}$,DE=$\sqrt{3}$,AD=2,
在△ADE中,由余弦定理得cos∠AED=$\frac{3+3-4}{2•\sqrt{3}•\sqrt{3}}$=$\frac{1}{3}$.
故选:A.
点评 本题考查求二面角的余弦值,涉及到余弦定理等知识,注意解题方法的积累,属于中档题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 已知Rt△ABC的斜边BC在平面α内,两直角边AB、AC与平面α所成角分别为30°和45°.A在α上射影为E.
已知Rt△ABC的斜边BC在平面α内,两直角边AB、AC与平面α所成角分别为30°和45°.A在α上射影为E. 如图,在四面体ABCD中,E,F分别是棱AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,已知AB=CD=3,EF=$\sqrt{5}$,求异面直线AB和CD所成的角.
如图,在四面体ABCD中,E,F分别是棱AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,已知AB=CD=3,EF=$\sqrt{5}$,求异面直线AB和CD所成的角.