题目内容
正数数列{an}的前n项和为Sn,且2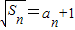 .
.(1)试求数列{an}的通项公式;
(2)设bn=
 ,{bn}的前n项和为Tn,若对一切正整数n都有Tn<m,求m的最小值.
,{bn}的前n项和为Tn,若对一切正整数n都有Tn<m,求m的最小值.
【答案】分析:(1)由an>0,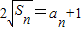 ,知4Sn=(an+1)2,4Sn-1=(an-1+1)2,由此能求出数列{an}的通项公式.
,知4Sn=(an+1)2,4Sn-1=(an-1+1)2,由此能求出数列{an}的通项公式.
(2)由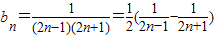 ,知
,知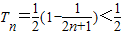 ,由此能求出m的最小值.
,由此能求出m的最小值.
解答:解:(1)∵an>0,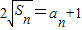 ,
,
∴4Sn=(an+1)2,4Sn-1=(an-1+1)2,
则当n≥2时,
4an=an2+2an-an-12-2an-1,
即(an+an-1)(an-an-1-2)=0,
而an>0,
∴an-an-1=2(n≥2)
又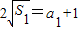 ,
,
∴a1=1,则an=2n-1
(2)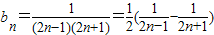 ,
,
∴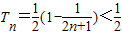 ,m≥
,m≥ .
.
所以m的最小值是 .
.
点评:本题考查数列的性质和应用,解题时要注意数列递推公式的合理运用.
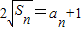 ,知4Sn=(an+1)2,4Sn-1=(an-1+1)2,由此能求出数列{an}的通项公式.
,知4Sn=(an+1)2,4Sn-1=(an-1+1)2,由此能求出数列{an}的通项公式.(2)由
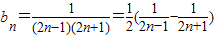 ,知
,知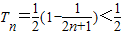 ,由此能求出m的最小值.
,由此能求出m的最小值.解答:解:(1)∵an>0,
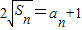 ,
,∴4Sn=(an+1)2,4Sn-1=(an-1+1)2,
则当n≥2时,
4an=an2+2an-an-12-2an-1,
即(an+an-1)(an-an-1-2)=0,
而an>0,
∴an-an-1=2(n≥2)
又
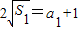 ,
,∴a1=1,则an=2n-1
(2)
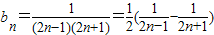 ,
,∴
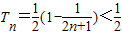 ,m≥
,m≥ .
.所以m的最小值是
 .
.点评:本题考查数列的性质和应用,解题时要注意数列递推公式的合理运用.

练习册系列答案
相关题目