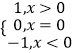Question

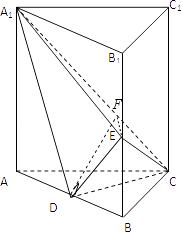
【题目】如图，直棱柱ABC﹣A1B1C1中，D，E分别是AB，BB1的中点，AA1=AC=CB= AB． （Ⅰ）证明：BC1∥平面A1CD；
（Ⅱ）求二面角D﹣A1C﹣E的余弦值．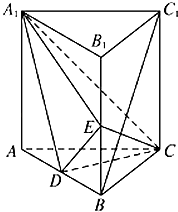

Answer 1

【答案】证明：（Ⅰ）连结AC1交A1C于点F，则F为AC1的中点， 又D是AB中点，连结DF，则BC1∥DF，
因为DF平面A1CD，BC1平面A1CD，
所以BC1∥平面A1CD．
（Ⅱ）解：因为直棱柱ABC﹣A1B1C1 ， 所以AA1⊥CD，
由已知AC=CB，D为AB的中点，所以CD⊥AB，
又AA1∩AB=A，于是，CD⊥平面ABB1A1 ，
设AB=2 ，则AA1=AC=CB=2，得∠ACB=90°，
CD= ，A1D= ，DE= ，A1E=3
故A1D2+DE2=A1E2 ， 即DE⊥A1D，所以DE⊥平面A1DC，
又A1C=2 ，过D作DF⊥A1C于F，∠DFE为二面角D﹣A1C﹣E的平面角，
在△A1DC中，DF= = ，EF= = ，
所以二面角D﹣A1C﹣E的余弦值cos∠DFE= = ．

【解析】（Ⅰ）通过证明BC1平行平面A1CD内的直线DF，利用直线与平面平行的判定定理证明BC1∥平面A1CD（Ⅱ）证明DE⊥平面A1DC，作出二面角D﹣A1C﹣E的平面角，然后求解二面角平面角的余弦值即可．
【考点精析】认真审题，首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)．