题目内容
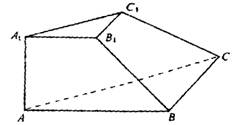
如图,在三棱台A1B1C1-ABC中,已知A1A⊥底面ABC,A1A= A1B1= B1C1=a,B1B⊥BC,且B1B和底面ABC所成的角45º,求这个棱台的体积.

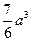 .
.解:因为A1A⊥底面ABC,所以根据平面的垂线的定义有A1A⊥BC.又BC⊥BB1,且棱AA1和BB1的延长线交于一点,所以利用直线和平面垂直的判定定理可以推出BC⊥侧面A1ABB1,从而根据平面的垂线的定义又可得出BC⊥AB.
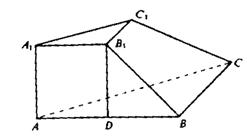
∴△ABC是直角三角形,∠ABC=90º.并且∠ABB1就是BB1和底面ABC所成的角,
∠ABB1=45º. ——3分
作B1D⊥AB交AB于D,则B1D∥A1A,故B1D⊥底面ABC.
∵ Rt△B1DB中∠DBB1=45º,
∴DB=DB1=AA1=a,
∴AB=2a. ——6分
由于棱台的两个底面相似,故
Rt△ABC∽Rt△A1B1C1.
∵B1C1=A1B1=a,AB=2a,
∴BC=2a.
∴S上=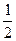 A1B1×B1C1=
A1B1×B1C1=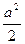 .
.
S下=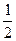 AB×BC=2a2. ——8分
AB×BC=2a2. ——8分
V棱台=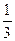 ·A1A·
·A1A·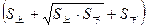
=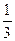 ·a·
·a·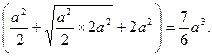 ——10分
——10分

∴△ABC是直角三角形,∠ABC=90º.并且∠ABB1就是BB1和底面ABC所成的角,
∠ABB1=45º. ——3分
作B1D⊥AB交AB于D,则B1D∥A1A,故B1D⊥底面ABC.
∵ Rt△B1DB中∠DBB1=45º,
∴DB=DB1=AA1=a,
∴AB=2a. ——6分
由于棱台的两个底面相似,故
Rt△ABC∽Rt△A1B1C1.
∵B1C1=A1B1=a,AB=2a,
∴BC=2a.
∴S上=
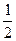 A1B1×B1C1=
A1B1×B1C1=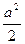 .
.S下=
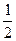 AB×BC=2a2. ——8分
AB×BC=2a2. ——8分V棱台=
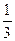 ·A1A·
·A1A·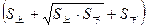
=
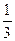 ·a·
·a·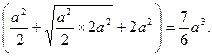 ——10分
——10分
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
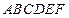 中,已知平面
中,已知平面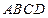 是边长为
是边长为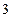 的正方形,
的正方形,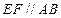 ,
,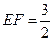 ,且
,且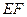 与平面
与平面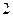 ,则该多面体的体积为( )
,则该多面体的体积为( )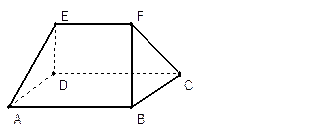
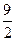
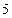
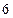
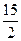
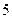 ,它的对角线的长
,它的对角线的长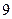 和
和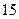 ,则这个棱柱的侧面积是( )
,则这个棱柱的侧面积是( ) 
 ,
,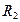 ,
,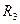 满足
满足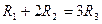 ,则它们的表面积
,则它们的表面积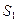 ,
,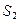 ,
,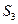 ,满足的等量关系是___________.
,满足的等量关系是___________.