题目内容
【题目】已知直线![]() 的参数方程为:
的参数方程为: ![]() ,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 和曲线C的普通方程;
和曲线C的普通方程;
(2)在直角坐标系中,过点B(0,1)作直线![]() 的垂线,垂足为H,试以
的垂线,垂足为H,试以![]() 为参数,求动点H轨迹的参数方程,并指出轨迹表示的曲线.
为参数,求动点H轨迹的参数方程,并指出轨迹表示的曲线.
【答案】(1)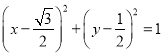 .(2)圆心在原点,半径为1的圆.
.(2)圆心在原点,半径为1的圆.
【解析】试题分析:(1)根据三角函数同角关系: ![]() 消参数得直线
消参数得直线![]() 的普通方程,根据
的普通方程,根据![]() 将曲线C的极坐标方程化为直角坐标方程,(2)先根据垂直关系求直线
将曲线C的极坐标方程化为直角坐标方程,(2)先根据垂直关系求直线![]() 的垂线方程,再利用方程组解出垂足H坐标,最后根据三角函数同角关系:
的垂线方程,再利用方程组解出垂足H坐标,最后根据三角函数同角关系: ![]() 消参数得动点H的普通方程,根据方程类型确定曲线形状.
消参数得动点H的普通方程,根据方程类型确定曲线形状.
试题解析:(1)由![]() ,
,
消去t得,直线![]() 的普通方程:
的普通方程: ![]() .
.
由![]() 得,
得, ![]() ,
,
即![]() ,得曲线C的普通方程:
,得曲线C的普通方程: 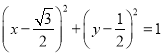 .
.
(2)∵直线![]() 的普通方程:
的普通方程: ![]() ,又BH⊥
,又BH⊥![]() ,
,
∴直线BH的方程为![]() ,
,
由上面两个方程解得: ![]() ,
,
即动点H的参数方程为: ![]() 表示圆心在原点,半径为1的圆.
表示圆心在原点,半径为1的圆.

 全能练考卷系列答案
全能练考卷系列答案【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如下图所示(![]() (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;

(Ⅱ)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店准备一次性买进25吨,则预计需要销售多少天.
参考公式:  ,
, ![]() .
.
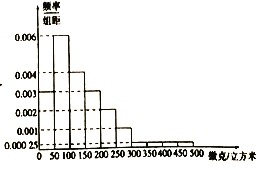
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.