题目内容
【题目】如图所示的多面体中,四边形ABCD为菱形,![]() ,
,![]() ,
,![]() 面ABCD,
面ABCD,![]() ,
,![]() ,异面直线AF,CD所成角的余弦值为
,异面直线AF,CD所成角的余弦值为![]() .
.

![]() Ⅰ
Ⅰ![]() 求证:面
求证:面![]() 面EDB;
面EDB;
![]() Ⅱ
Ⅱ![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 推导出
推导出![]() ,从而
,从而![]() ,进而
,进而![]() 面EBD,由此能证明面
面EBD,由此能证明面![]() 面EDB;
面EDB;![]() Ⅱ
Ⅱ![]() 推导出四边形EFOD是平行四边形,从而
推导出四边形EFOD是平行四边形,从而![]() ,由
,由![]() 面ABCD,得
面ABCD,得![]() 面ABCD,以O为原点,OA,OB,OF分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角
面ABCD,以O为原点,OA,OB,OF分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
![]() Ⅰ
Ⅰ![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() ,
,

![]() 面ABCD,
面ABCD,![]() 面ABCD,
面ABCD,![]() ,
,
![]() ,
,![]() 面EBD,
面EBD,
![]() 面ACF,
面ACF,![]() 面
面![]() 面EDB.
面EDB.
![]() Ⅱ
Ⅱ![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 四边形EFOD是平行四边形,
四边形EFOD是平行四边形,![]() ,
,
![]() 面ABCD,
面ABCD,![]() 面ABCD,
面ABCD,
以O为原点,OA,OB,OF分别为x,y,z轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() 0,
0,![]() ,设
,设![]() 0,
0,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
解得![]() ,则
,则![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,
![]() 1,
1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面AFB的法向量![]() y,
y,![]() ,
,
则 ,取
,取![]() ,得
,得![]() ,
,
设平面AFE的法向量![]() y,
y,![]() ,
,
则 ,取
,取![]() ,得
,得![]() 0,
0,![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,由图形得
,由图形得![]() 为钝角,
为钝角,
则![]() .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: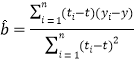 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)

