题目内容
【题目】已知椭圆E： 
+ 
=1（a＞b＞0）经过点（﹣1， 
），其离心率e= 
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设动直线l：y=kx+m与椭圆C相切，切点为T，且l与直线x=﹣4相交于点S．
试问：在x轴上是否存在一定点，使得以ST为直径的圆恒过该定点？若存在，求出该点的坐标；若不存在，请说明理由．
【答案】解：（Ⅰ）由点（1， 
）在椭圆上得，代入椭圆方程： 
，①﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
椭圆的离心率e= 
= 
，则a=2c，a2=4c2 ， b2=3c2 ， ②
②代入①解得c2=1，a2=4，b2=3，
故椭圆C的标准方程为 
；
（Ⅱ）由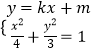 
，消去y，整理得（4k2+3）x2+8kmx+4m2﹣12=0；
因为动直线l与椭圆C相切，即它们有且只有一个公共点T，可设T（x0 ， y0），
m≠0，△=0，∴（8km）2﹣4×（4k2+3）×（4m2﹣12）=0，
∴4k2﹣m2+3=0，③﹣﹣﹣﹣
此时，x0= 
=﹣ 
=﹣ 
，y0=kx0+m= 
，则T（﹣ ， ）．由 
，得S（4，4k+m）．假设平面内存在定点满足条件，不妨设为点A．
由图形对称性知，点A必在x轴上．设A（x1 ， 0），则由已知条件知AS⊥AT，
即 
=0对满足③式的m，k恒成立．由 =（4﹣x1 ， 4k+m）， =（﹣ ﹣x1 ， ），由 =0得：﹣ 
+ 
﹣4x1+x12+ 
+3=0，
整理得（4x1﹣4） 
+x12﹣4x1+3=0，④由②式对满足①式的m，k恒成立，则 
，解得x1=1．
故平面内存在定点（1，0），使得以ST为直径的圆恒过该定点．
【解析】（Ⅰ）由题意可知：将点代入椭圆方程，利用椭圆的离心率公式即可求得a和b的值，即可求得椭圆方程；（Ⅱ）将直线方程代入椭圆方程，由△=0，求得4k2﹣m2+3=0，利用韦达定理及中点坐标公式，求得T点坐标，联立即可求得S点坐标，由 =0，根据向量数量积的坐标运算，可得 ，即可求得A点坐标，即可求得以ST为直径的圆恒过该定点（1，0）．
