题目内容
设函数 ,
, ,其中实数
,其中实数 .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)当函数 与
与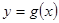 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 的最小值为
的最小值为 ,求
,求 的值域;
的值域;
(3)若 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
(1)详见解析;(2)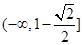 ;(3)
;(3)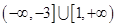 .
.
解析试题分析:(1)这是一个三次函数求单调区间的问题,此类问题比较熟悉,三次函数的导数为二次函数,它的零点容易求出,但要注意对零点大小的比较,才能准确写出单调区间;(2)函数 与
与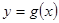 的图象只有一个公共点,知方程
的图象只有一个公共点,知方程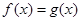 只有一个根(含重根),结合
只有一个根(含重根),结合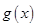 有最小值,可求出
有最小值,可求出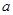 的取值范围,而
的取值范围,而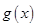 是一个二次函数,易得它提最小值
是一个二次函数,易得它提最小值 ,最后可求出
,最后可求出 的值域;(3)由(1)的过程和结果易知
的值域;(3)由(1)的过程和结果易知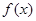 的单调增区间,
的单调增区间, 应是其子区间,再由
应是其子区间,再由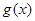 的单调增区间,
的单调增区间, 也应是其子区间,从而确定
也应是其子区间,从而确定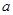 的取值范围,要注意分类讨论思想的应用.
的取值范围,要注意分类讨论思想的应用.
试题解析:(1)∵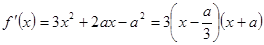 ,又
,又
∴当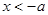 或
或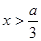 时,
时,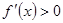 ;当
;当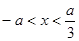 时,
时,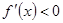
∴ 的递增区间为
的递增区间为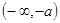 和
和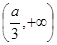 ,递减区间为
,递减区间为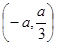 .
.
(2)由题意知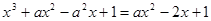
即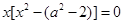 恰有一根(含重根)∴
恰有一根(含重根)∴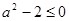 ,即
,即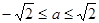 ,
,
又 ,且
,且 存在最小值,所以
存在最小值,所以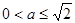
又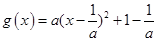 ,∴
,∴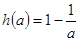 ,∴
,∴ 的值域为
的值域为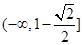 .
.
(3)当 时,
时, 在
在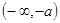 和
和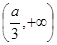 内是增函数,
内是增函数, 在
在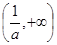 内是增函数,由题意得
内是增函数,由题意得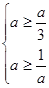 ,解得
,解得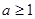 .
.
当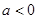 时,
时, 在
在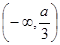 和
和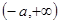 内是增函数,
内是增函数, 在
在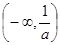 内是增函数,由题意得
内是增函数,由题意得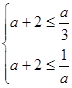 ,解得
,解得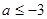 .
.
综上可知,实数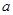 的取值范围为
的取值范围为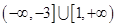 .
.
考点:函数的综合应用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
某市一家庭今年一月份、二月份、和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
若每月用气量不超过最低额度
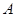
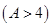 立方米时,只付基本费3元+每户每月定额保险费
立方米时,只付基本费3元+每户每月定额保险费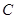
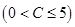 元;若用气量超过
元;若用气量超过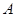 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付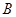 元.
元.⑴根据上面的表格求
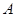 、
、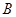 、
、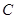 的值;
的值;⑵若用户第四月份用气30立方米,则应交煤气费多少元?

 在[-3,2]上具有单调性,求实数
在[-3,2]上具有单调性,求实数 的取值范围。
的取值范围。 有最小值为-12,求实数
有最小值为-12,求实数 ;
;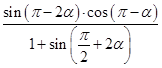 .
. 的解集为M.
的解集为M. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数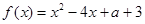 ,
,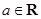 .
. 的图象与
的图象与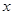 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;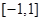 上存在零点,求
上存在零点,求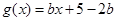 ,
,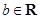 .当
.当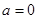 时,若对任意的
时,若对任意的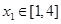 ,总存在
,总存在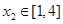 ,使得
,使得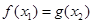 ,求
,求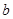 的取值范围.
的取值范围.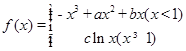 的图像在点
的图像在点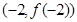 处的切线方程为
处的切线方程为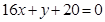 .
.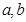 的值;
的值; 在区间
在区间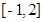 上的最大值;
上的最大值;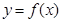 上存在两点
上存在两点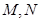 使得
使得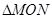 是以坐标原点
是以坐标原点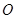 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边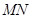 的中点在
的中点在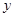 轴上,求实数
轴上,求实数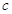 的取值范围.
的取值范围. .
.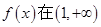 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;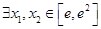 ,使
,使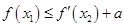 成立,求实数a的取值范围.
成立,求实数a的取值范围. 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 上的最大值为12.
上的最大值为12. 上的最小值为
上的最小值为 ,求
,求