题目内容
6.已知向量$\overrightarrow{m}$,$\overrightarrow{n}$的夹角为60°,且|$\overrightarrow{m}$|=1,|$\overrightarrow{n}$|=2,又$\overrightarrow{a}$=2$\overrightarrow{m}$+$\overrightarrow{n}$,$\overrightarrow{b}$=-3$\overrightarrow{m}$+$\overrightarrow{n}$(Ⅰ)求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦;
(Ⅱ)设$\overrightarrow{c}$=t$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{d}$=$\overrightarrow{m}$-$\overrightarrow{n}$,若$\overrightarrow{c}$⊥$\overrightarrow{d}$,求实数t的值.
分析 (Ⅰ)进行数量积的运算便可得出$\overrightarrow{a}•\overrightarrow{b}=-3$,根据$|\overrightarrow{a}|=\sqrt{(2\overrightarrow{m}+\overrightarrow{n})^{2}}$便可求出$|\overrightarrow{a}|$,同理可求出$|\overrightarrow{b}|$,这样根据向量夹角的余弦公式即可求出$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦;
(Ⅱ)先求出$\overrightarrow{c}=(2t+3)\overrightarrow{m}+(t-1)\overrightarrow{n}$,而根据$\overrightarrow{c}⊥\overrightarrow{d}$便有$\overrightarrow{c}•\overrightarrow{d}=[(2t+3)\overrightarrow{m}+(t-1)\overrightarrow{n}]•[(t-1)\overrightarrow{n}]=0$,进行数量积的运算即可求出t的值.
解答 解:(Ⅰ)$\overrightarrow{a}•\overrightarrow{b}=(2\overrightarrow{m}+\overrightarrow{n})•(-3\overrightarrow{m}+\overrightarrow{n})$=$-6{\overrightarrow{m}}^{2}-\overrightarrow{m}•\overrightarrow{n}+{\overrightarrow{n}}^{2}$=-6-1•2•cos60°+4=-3;
$|\overrightarrow{a}|=\sqrt{(2\overrightarrow{m}+\overrightarrow{n})^{2}}=\sqrt{4{\overrightarrow{m}}^{2}+4\overrightarrow{m}•\overrightarrow{n}+{\overrightarrow{n}}^{2}}$=$\sqrt{4+4+4}=2\sqrt{3}$,$|\overrightarrow{b}|=\sqrt{(-3\overrightarrow{m}+\overrightarrow{n})^{2}}=\sqrt{9-6+4}=\sqrt{7}$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{-3}{2\sqrt{3}•\sqrt{7}}=-\frac{\sqrt{21}}{14}$;
即$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦为$-\frac{\sqrt{21}}{14}$;
(Ⅱ)$\overrightarrow{c}=t(2\overrightarrow{m}+\overrightarrow{n})-(-3\overrightarrow{m}+\overrightarrow{n})=(2t+3)\overrightarrow{m}$$+(t-1)\overrightarrow{n}$,$\overrightarrow{c}⊥\overrightarrow{d}$;
∴$\overrightarrow{c}•\overrightarrow{d}=(2t+3){\overrightarrow{m}}^{2}-(t+4)\overrightarrow{m}•\overrightarrow{n}-(t-1){\overrightarrow{n}}^{2}$=2t+3-t-4-4t+4=0;
∴t=1.
点评 考查向量数量积的运算及其计算公式,求向量长度的方法:根据$|\overrightarrow{a}|=\sqrt{{\overrightarrow{a}}^{2}}$,向量夹角的余弦公式,向量的减法和数乘运算,向量垂直的充要条件.

| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
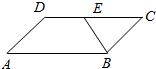 如图,在平行四边形ABCD中,E是CD中点,$\overrightarrow{BE}=x\overrightarrow{AB}+y\overrightarrow{AD}$,则x+y=$\frac{1}{2}$.
如图,在平行四边形ABCD中,E是CD中点,$\overrightarrow{BE}=x\overrightarrow{AB}+y\overrightarrow{AD}$,则x+y=$\frac{1}{2}$.