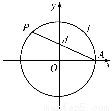
题目内容
在平面直角坐标系xOy中，已知对于任意实数k，直线(
k＋1)x＋(k－
)y－(3k＋
)＝0恒过定点F.设椭圆C的中心在原点，一个焦点为F，且椭圆C上的点到F的最大距离为2＋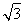
.
(1)求椭圆C的方程；
(2)设(m，n)是椭圆C上的任意一点，圆O：x2＋y2＝r2(r＞0)与椭圆C有4个相异公共点，试分别判断圆O与直线l1：mx＋ny＝1和l2：mx＋ny＝4的位置关系．
（1）
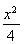＋y2＝1.（2）直线l1与圆O相交，直线l2与圆O相离．
【解析】(1)由(
k＋1)x＋(k－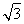
)y－(3k＋
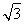)＝0整理
得(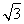
x＋y－3)k＋(x－
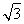y－
)＝0，
解方程组
得F(
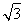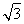，0)．
设椭圆C的长轴长、短轴长、焦距分别为2a,2b,2c，则由题设知
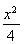于是a＝2，b＝1. 所以椭圆C的方程为＋y2＝1.
(2)因为圆O：x2＋y2＝r2(r＞0)与椭圆C有4个相异公共点，所以b＜r＜a，即1＜r＜2.
因为点(m，n)是椭圆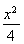
＋y2＝1上的点，所以
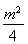＋n2＝1，
且－2≤m≤2.所以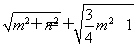
∈[1,2]．
于是圆心O到直线l1的距离d1＝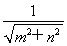
≤1＜r，
圆心O到直线l2的距离d2＝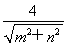
≥2＞r.
故直线l1与圆O相交，直线l2与圆O相离
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
