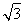题目内容
如图，在四棱锥O ?ABCD中，底面ABCD为菱形，OA⊥平面ABCD，E为OA的中点，F为BC的中点，求证：(1)平面BDO⊥平面ACO；(2)EF∥平面OCD.
见解析
【解析】
证明 (1)∵OA⊥平面ABCD，BD?平面ABCD，所以OA⊥BD，
∵ABCD是菱形，∴AC⊥BD，又OA∩AC＝A，∴BD⊥平面OAC，
又∵BD?平面OBD，∴平面BDO⊥平面ACO.
(2)取OD中点M，连接EM，CM，则ME∥AD，ME＝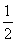
AD，
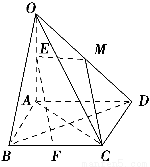
∵ABCD是菱形，∴AD∥BC，AD＝BC，
∵F为BC的中点，∴CF∥AD，CF＝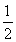
AD，
∴ME∥CF，ME＝CF.∴四边形EFCM是平行四边行，
∴EF∥CM，
又∵EF?平面OCD，CM?平面OCD.
∴EF∥平面OCD.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
