题目内容

（2012•河北模拟）计算
tan(
π
4
+a)•cos2a
2cos2(
π
4
-a)
的值为（　　）
分析：利用互余两角正余弦的关系，将分母cos（
π
4
-α）化成sin（
π
4
+α），再将tan（
π
4
+α）化成正弦除以余弦，进行约分化简，最后用
π
2
+α的诱导公式化简，可得分子与分母相同，故原式的值为1．
解答：解：∵
π
4
+α与
π
4
-α互余，∴cos（
π
4
-α）=sin（
π
4
+α）
∴原式=tan（
π
4
+α）•
cos2α
2sin2(
π
4
+α)
=
sin(
π
4
+α)
cos(
π
4
+α)
•
cos2α
2sin2(
π
4
+α)
=
cos2α
2sin (
π
4
+α)cos(
π
4
+α)
=
cos2α
sin (
π
2
+2α)

∵sin（
π
2
+α）=cosα，
∴
cos2α
sin (
π
2
+2α)
=
cos2α
cos 2α
=1，即原式=1
故选D
点评：本题将一个三角函数的分式化简整理，从而求出它的值，考查了同角三角函数的关系和诱导公式，以及二倍角的正弦公式等知识，属于基础题．
练习册系列答案
相关题目
（2012•河北模拟）已知函数f（x）=xlnx，g（x）=-x2+ax-2
（Ⅰ）求函数f（x）在[t，t+2]（t＞0）上的最小值；
（Ⅱ）若函数y=f（x）+g（x）有两个不同的极值点x1，x2（x1＜x2）且x2-x1＞ln2，求实数a的取值范围．
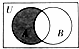（2012•河北模拟）设全集U=R，A={x|2(x-1)2＜2}，B={x|log
1
2
(x2+x+1)＞-log2(x2+2)}，则图中阴影部分表示的集合为（　　）
（2012•河北模拟）如图是一个程序框图，该程序框图输出的结果是
4
5
，则判断框内应该填入的是（　　）
（2012•河北模拟）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其导函数f'（x）的部分图象如图所示，则函数f（x）的解析式为（　　）
（2012•河北模拟）定义在[1，+∞）上的函数f（x）满足：①f（2x）=cf（x）（c为正常数）；②当2≤x≤4时，f（x）=1-（x-3）2，若函数f（x）的图象上所有极大值对应的点均落在同一条直线上，则c等于（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网