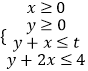Question

【题目】已知函数是定义在实数集上的奇函数，当时， ，若集合，则实数的取值范围是______.

Answer 1

【答案】

【解析】

把x≥0时的f（x）改写成分段函数，求出其最小值，由函数的奇偶性可得x＜0时的函数的最大值，条件等价为对x∈R，都有f（x-1）f（x），进行转化求解即可求解该不等式得答案．

若=，
则等价为f（x-1）-f（x） 0恒成立，即f（x-1）f（x）恒成立，
当x≥0时 ．
若a≤0，

则当x≥0时， ，
∵f（x）是奇函数，
∴若x＜0，则-x＞0，则f（-x）=-x=-f（x），
则f（x）=x，x＜0，
综上f（x）=x，此时函数为增函数，则f（x-1）f（x）恒成立；
若a＞0，
若0≤x≤a时， ；
当a＜x≤2a时， ；
当x＞2a时， ．即当x≥0时，函数的最小值为-a，
由于函数f（x）是定义在R上的奇函数，
当x＜0时，f（x）的最大值为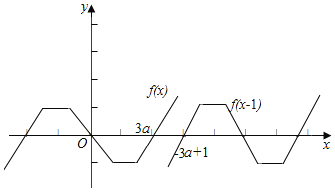a，
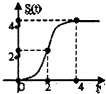
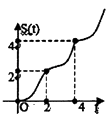
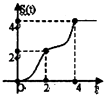
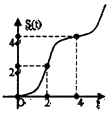
作出函数的图象如图：
由于x∈R，f（x-1）f（x），
故函数f（x-1）的图象不能在函数f（x）的图象的上方，
结合图可得 ，即6a2，求得0＜a ，
综上a ，
故答案为：