题目内容
【题目】已知函数![]() 。
。
(1)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(2)若![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若对任意的
,若对任意的![]()
恒有![]() ,求
,求![]() 的取值范围(
的取值范围(![]() 是自然对数的底数)。
是自然对数的底数)。
【答案】(1) 当![]() 时,
时, ![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2) ![]()
【解析】试题分析:
(1)求导数,分![]() 三种情况分别讨论导函数的符号,从而得到函数的单调情况。(2)根据导数的几何意义可得
三种情况分别讨论导函数的符号,从而得到函数的单调情况。(2)根据导数的几何意义可得![]() ,从而
,从而![]() 。故由题意得
。故由题意得![]() 对任意的
对任意的![]() 恒成立。设
恒成立。设![]() ,
, ![]() ,根据单调性可求得
,根据单调性可求得![]() ,从而可得
,从而可得![]() 。
。
试题解析:
(1)当![]() 时,
时, ![]() ,
,
所以![]() 。
。
令![]() ,解得
,解得![]() 或
或![]() ,
,
①当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时, ![]() ,列表得:
,列表得:

所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
③当![]() 时,
时, ![]() ,列表得:
,列表得:

所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。
上单调递减。
综上可得,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。
上单调递减。
(2)因为![]() ,
,
所以![]() ,
,
由题意得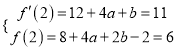 ,
,
整理得![]() ,解得
,解得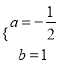
所以![]() ,
,
因为![]() 对任意的
对任意的![]() 恒成立,
恒成立,
所以![]() 对任意的
对任意的![]() 恒成立,
恒成立,
设![]() ,
,
则![]() ,
,
所以当![]() 时,
时, ![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() 单调递增。
单调递增。
因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
解得![]() 。
。
所以实数![]() 的取值范围为
的取值范围为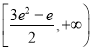 。
。

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x单位:小时)与当天投篮命中率y之间的关系:
时间x | 1 | 2 | 3 | 4 | 5 |
命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(1)求小李这5天的平均投篮命中率;
(2)用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.  .
.