��Ŀ����
��֪����B1��1��y1����B2��2��y2��������Bn��n��yn��������n��N*��˳��Ϊֱ��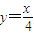 �ϵĵ㣬����A1��x1��0����A2��x2��0��������An��xn��0��������n��N*��˳��Ϊx���ϵĵ㣬����x1=a��0��a��1�����������n��N*����An��Bn��An+1������BnΪ����ĵ��������Σ�
�ϵĵ㣬����A1��x1��0����A2��x2��0��������An��xn��0��������n��N*��˳��Ϊx���ϵĵ㣬����x1=a��0��a��1�����������n��N*����An��Bn��An+1������BnΪ����ĵ��������Σ�������֤���������n��N*��xn+2-xn�dz�������������{xn}��ͨ�ʽ��
�������Ƿ���ڵ���ֱ��������AnBnAn+1����˵�����ɣ�
���𰸡������������ɵ�An��Bn��An+1������BnΪ����ĵ��������Σ�����|AnBn|=|An+1Bn|�õ�xn+1+xn=2n���Ӷ���xn+2+xn+1=2��n+1����ʽ������⣮
��������ڵ���ֱ��������AnBnAn+1������Rt��AnBnAn+1�У�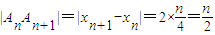 ����nΪ������ʱ��|xn+1-xn|=2��1-a��������
����nΪ������ʱ��|xn+1-xn|=2��1-a��������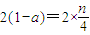 ����
����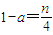 ��0��n��4��n=1��3ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���nΪ��ż��ʱ��|xn+1-xn|��
��0��n��4��n=1��3ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���nΪ��ż��ʱ��|xn+1-xn|��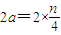 ����
����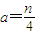 ����n=2ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ�
����n=2ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ�
����⣺�����������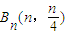 ��An��xn��0����An+1��xn+1��0����
��An��xn��0����An+1��xn+1��0����
�ߵ�An��Bn��An+1������BnΪ����ĵ��������Σ�
��|AnBn|=|An+1Bn|����
��xn2-2nxn=xn+12-2nxn+1⇒��xn+1-xn����xn+1+xn��=2n��xn+1-xn��
�֡�xn+1��xn����xn+1+xn=2n����
��xn+2+xn+1=2��n+1����
�ɢ�-�ٵã�xn+2-xn=2����xn+2-xn�dz�������6�֣�
������{x2k-1}��{x2k}��k��N*�����ǵȲ����У�
��ע������ֱ����ͼ��õ�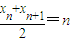 ����xn+xn+1=2n����n��N*����
����xn+xn+1=2n����n��N*����
��nΪ������ʱ��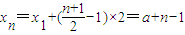 ��
��
��nΪ��ż��ʱ����x2+x1=2�ã�x2=2-a����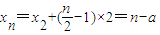 ��
��
��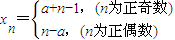 ����8�֣�
����8�֣�
��������ڵ���ֱ��������AnBnAn+1���������AnBnAn+1=90°��
��Rt��AnBnAn+1�У�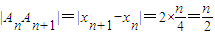 ����10�֣�
����10�֣�
��nΪ������ʱ��xn=a+n-1��xn+1=n+1-a��
��|xn+1-xn|=|n+1-a-a-n+1|=|2-2a|=2��1-a��������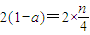 ����
����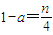 ��
��
�֡�0��a��1����0��1-a��1����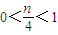 ����0��n��4��
����0��n��4��
�൱n=1��3ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���12�֣�
��nΪ��ż��ʱ��xn=n-a��xn+1=a+n+1-1=a+n��
��|xn+1-xn|=|a+n-n+a|=|2a|=2a������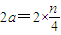 ����
���� ��
��
�֡�0��a��1����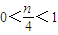 ����0��n��4��
����0��n��4��
�൱n=2ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���14�֣�
������������n=1��2��3ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���16�֣�
������������Ҫ����������������е��ۺ����⣬�漰�������е�ͨ�ʽ�������ľ��빫ʽ�Լ��������ۣ����ν�ϵ�˼�룮
��������ڵ���ֱ��������AnBnAn+1������Rt��AnBnAn+1�У�
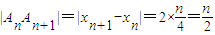 ����nΪ������ʱ��|xn+1-xn|=2��1-a��������
����nΪ������ʱ��|xn+1-xn|=2��1-a��������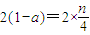 ����
����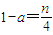 ��0��n��4��n=1��3ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���nΪ��ż��ʱ��|xn+1-xn|��
��0��n��4��n=1��3ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���nΪ��ż��ʱ��|xn+1-xn|��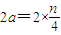 ����
����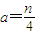 ����n=2ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ�
����n=2ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ�����⣺�����������
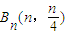 ��An��xn��0����An+1��xn+1��0����
��An��xn��0����An+1��xn+1��0�����ߵ�An��Bn��An+1������BnΪ����ĵ��������Σ�
��|AnBn|=|An+1Bn|����

��xn2-2nxn=xn+12-2nxn+1⇒��xn+1-xn����xn+1+xn��=2n��xn+1-xn��
�֡�xn+1��xn����xn+1+xn=2n����
��xn+2+xn+1=2��n+1����
�ɢ�-�ٵã�xn+2-xn=2����xn+2-xn�dz�������6�֣�
������{x2k-1}��{x2k}��k��N*�����ǵȲ����У�
��ע������ֱ����ͼ��õ�
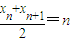 ����xn+xn+1=2n����n��N*����
����xn+xn+1=2n����n��N*������nΪ������ʱ��
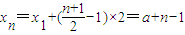 ��
����nΪ��ż��ʱ����x2+x1=2�ã�x2=2-a����
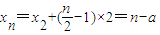 ��
����
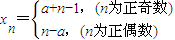 ����8�֣�
����8�֣���������ڵ���ֱ��������AnBnAn+1���������AnBnAn+1=90°��
��Rt��AnBnAn+1��
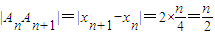 ����10�֣�
����10�֣���nΪ������ʱ��xn=a+n-1��xn+1=n+1-a��
��|xn+1-xn|=|n+1-a-a-n+1|=|2-2a|=2��1-a��������
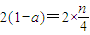 ����
����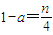 ��
���֡�0��a��1����0��1-a��1����
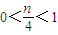 ����0��n��4��
����0��n��4���൱n=1��3ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���12�֣�
��nΪ��ż��ʱ��xn=n-a��xn+1=a+n+1-1=a+n��
��|xn+1-xn|=|a+n-n+a|=|2a|=2a������
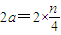 ����
���� ��
���֡�0��a��1����
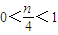 ����0��n��4��
����0��n��4���൱n=2ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���14�֣�
������������n=1��2��3ʱ��ʹ��������AnBnAn+1Ϊ����ֱ�������Σ���16�֣�
������������Ҫ����������������е��ۺ����⣬�漰�������е�ͨ�ʽ�������ľ��빫ʽ�Լ��������ۣ����ν�ϵ�˼�룮

��ϰ��ϵ�д�
 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
�����Ŀ
 ��֪����B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���y=
��֪����B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���y= ��֪����B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���
��֪����B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���