��Ŀ����
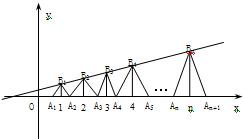
 ��֪����B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���y=
��֪����B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���y=| 1 |
| 4 |
| 1 |
| 12 |
��1��������{yn}2��ͨ�ʽ����֤��{yn}3�ǵȲ����У�
��2��֤��xn+2-xn5Ϊ���������������{xn}6��ͨ�ʽ��
��3������������������An8Bn9An+110�У��Ƿ����ֱ�������Σ����У������ʱaֵ���������ڣ���˵�����ɣ�
��������1�����õ���B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���y=
x+
���ɵ�����{yn}��ͨ�ʽ��������{yn}�ǵȲ����У�
��2�����ݡ�AnBnAn+1���An+1Bn+1An+2Ϊ���������Σ��ɵ�
����ʽ����������������{xn}��ͨ�ʽ��
��3��Ҫʹ��AnBnAn+1Ϊֱ�������Σ���xn+1-xn=2(
+
)�����ݣ�2����nΪ������ż��ʱ���������ۣ������ʱaֵ��
| 1 |
| 4 |
| 1 |
| 12 |
��2�����ݡ�AnBnAn+1���An+1Bn+1An+2Ϊ���������Σ��ɵ�
|
��3��Ҫʹ��AnBnAn+1Ϊֱ�������Σ���xn+1-xn=2(
| n |
| 4 |
| 1 |
| 12 |
����⣺��1���ߵ���B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���y=
x+
��yn=
n+
��yn+1-yn=
��{yn}�ǵȲ����У�
��2���ߡ�AnBnAn+1���An+1Bn+1An+2Ϊ����������
��
����xn+2-xn=2
��xn=
��3��Ҫʹ��AnBnAn+1Ϊֱ�������Σ���xn+1-xn=2(
+
)
��nΪ����ʱ��xn+1-xn=2��1-a������2(
+
)=2(1-a)
��a=
-
(n������0��a��1)
n=1����a=
��n=3��a=
��n��5�����⣻
��nΪż��ʱ��ͬ����a=
(nΪż����0��a��1)
n=2���� a=
��n��4�����⣻
�����ֱ�������Σ���ʱaֵΪ
��
��
| 1 |
| 4 |
| 1 |
| 12 |
��yn=
| 1 |
| 4 |
| 1 |
| 12 |
��yn+1-yn=
| 1 |
| 4 |
��{yn}�ǵȲ����У�
��2���ߡ�AnBnAn+1���An+1Bn+1An+2Ϊ����������
��
|
��xn=
|
��3��Ҫʹ��AnBnAn+1Ϊֱ�������Σ���xn+1-xn=2(
| n |
| 4 |
| 1 |
| 12 |
��nΪ����ʱ��xn+1-xn=2��1-a������2(
| n |
| 4 |
| 1 |
| 12 |
��a=
| 11 |
| 12 |
| n |
| 4 |
n=1����a=
| 2 |
| 3 |
| 1 |
| 6 |
��nΪż��ʱ��ͬ����a=
| 1 |
| 12 |
| n |
| 4 |
n=2���� a=
| 7 |
| 12 |
�����ֱ�������Σ���ʱaֵΪ
| 2 |
| 3 |
| 1 |
| 6 |
| 7 |
| 12 |
�����������Ժ���Ϊ���壬��������֪ʶ���������е�ͨ������������˼�룬�н�ǿ���ۺ��ԣ�

��ϰ��ϵ�д�
�����Ŀ
 ��֪����B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���y=
��֪����B1��1��y1����B2��2��y2��������Bn��n��yn����n��N��˳��Ϊһ�κ���y=