题目内容
【题目】若定义在R上的函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,则函数
,则函数![]() 在区间[-7,1]上的零点个数为( )
在区间[-7,1]上的零点个数为( )
A. 4 B. 6 C. 8 D. 10
【答案】C
【解析】定义在R上的函数f(x)满足f(x)=f(x),f(2x)=f(x),
∴函数f(x)是偶函数,且函数的图象关于x=1对称。
∵设g(x)=xex,其定义域为R,g′(x)=(xex)′=x′ex+x(ex)′=ex+xex
令g′(x)=ex+xex=ex(1+x)=0,解得:x=1.
列表:
x | (∞,1) | 1 | (1,+∞) |
g′(x) | 0 | + | |
g(x) | ↓ | 极小值 | ↑ |
由表可知函数g(x)=xex的单调递减区间为(∞,1),单调递增区间为(1,+∞).
当x=1时,函数g(x)=xex的极小值为![]() .
.
故函数y=|xex|在x=1时取得极大值为![]() ,
,
且y=|xex|在(∞,1)上是增函数,在(1,∞)上是减函数,
在区间[7,1]上,故当x<0时,f(x)与g(x)有7个交点,当x>0时,有1个交点,共有8个交点,
如图所示:
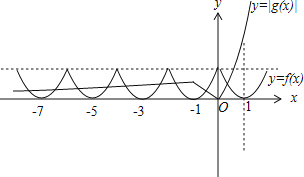
故选:C.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目