ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋžŨĄĒŌŌĄĒąûČýČËÍķĀšĩÄËŪÆ―ķžąČ―ÏÎČķĻĢŽČôČýČËļũŨÔķĀÁĒĩØ―øÐÐŌŧīÎÍķĀšēâĘÔĢŽÔōžŨÍķÖÐķøŌŌēŧÍķÖÐĩÄļÅÂĘΊ ![]() ĢŽŌŌÍķÖÐķøąûēŧÍķÖÐĩÄļÅÂĘΊ
ĢŽŌŌÍķÖÐķøąûēŧÍķÖÐĩÄļÅÂĘΊ ![]() ĢŽžŨĄĒąûÁ―ČËķžÍķÖÐĩÄļÅÂĘΊ
ĢŽžŨĄĒąûÁ―ČËķžÍķÖÐĩÄļÅÂĘΊ ![]() ĢŪ
ĢŪ
ĢĻ1ĢĐ·ÖąðĮóžŨĄĒŌŌĄĒąûČýČËļũŨÔÍķĀšŌŧīÎÍķÖÐĩÄļÅÂĘĢŧ
ĢĻ2ĢĐČôąûÁŽÐøÍķĀš5īÎĢŽĮóĮĄÓÐ2īÎÍķÖÐĩÄļÅÂĘĢŧ
ĢĻ3ĢĐČôąûÁŽÐøÍķĀš3īÎĢŽÃŋīÎÍķĀšĢŽÍķÖÐĩÃ2·ÖĢŽÎīÍķÖÐĩÃ0·ÖĢŽÔÚ3īÎÍķĀšÖÐĢŽČôÓÐ2īÎÁŽÐøÍķÖÐĢŽķøÁíÍâ1īÎÎīÍķÖÐĢŽÔōķîÍâžÓ1·ÖĢŧČô3īÎČŦÍķÖÐĢŽÔōķîÍâžÓ3·ÖĢŽžĮĶÎΊąûÁŽÐøÍķĀš3īΚóĩÄŨÜĩ÷ÖĢŽĮóĶÎĩÄ·ÖēžÁКÍÆÚÍûĢŪ
Ąūīð°ļĄŋ
ĢĻ1ĢĐ―âĢšžĮžŨĄĒŌŌĄĒąûČýČËļũŨÔķĀÁĒĩØ―øÐÐŌŧīÎÍķĀšēâĘÔÍķÖÐĩÄĘžþŌĀīÎΊAĄĒBĄĒCĢŽÓÉĖâÉčĖõžþÓÐĢš
![]() =
= ![]() ĢŽ
ĢŽ ![]() =
= ![]() ĢŽPĢĻACĢĐ=
ĢŽPĢĻACĢĐ= ![]() ĢŽžīPĢĻAĢĐ[1ĐPĢĻBĢĐ]=
ĢŽžīPĢĻAĢĐ[1ĐPĢĻBĢĐ]= ![]() ĢŽĒŲĢŧPĢĻBĢĐ[1ĐPĢĻCĢĐ]=
ĢŽĒŲĢŧPĢĻBĢĐ[1ĐPĢĻCĢĐ]= ![]() ĢŽĒÚPĢĻAĢĐPĢĻCĢĐ=
ĢŽĒÚPĢĻAĢĐPĢĻCĢĐ= ![]() ĢŽĒÛĢŪ
ĢŽĒÛĢŪ
ÓÉĒŲĒÛĩÃPĢĻBĢĐ=1Đ ![]() PĢĻCĢĐĢŽīúČëĒÚĩÃ27PĢĻCĢĐ]2Đ51PĢĻCĢĐ+22=0ĢŪ
PĢĻCĢĐĢŽīúČëĒÚĩÃ27PĢĻCĢĐ]2Đ51PĢĻCĢĐ+22=0ĢŪ
―âĩÃPĢĻCĢĐ= ![]() ŧōPĢĻCĢĐ=
ŧōPĢĻCĢĐ= ![]() ĢĻÉáČĨĢĐĢŪ―ŦPĢĻCĢĐ=
ĢĻÉáČĨĢĐĢŪ―ŦPĢĻCĢĐ= ![]() ·ÖąðīúČëĒÚĒÛŋÉĩÃPĢĻAĢĐ=
·ÖąðīúČëĒÚĒÛŋÉĩÃPĢĻAĢĐ= ![]() ĢŽPĢĻBĢĐ=
ĢŽPĢĻBĢĐ= ![]() ĢŪ
ĢŪ
đĘžŨĄĒŌŌĄĒąûČýČËļũŨÔÍķĀšŌŧīÎÍķÖÐĩÄļÅÂĘ·ÖąðĘĮ ![]() ĢŽ
ĢŽ ![]() ĢŽ
ĢŽ ![]()
ĢĻ2ĢĐ―âĢšąûÁŽÐøÍķĀš5īÎĢŽĮĄÓÐ2īÎÍķÖÐĩÄļÅÂĘΊ ![]()
ĢĻ3ĢĐ―âĢšĶÎŋÉŌÔČĄĩÄÖĩΊ0ĢŽ2ĢŽ4ĢŽ5ĢŽ9ĢŽŋÉĮóĩÃĢš ![]() ĢŽ
ĢŽ ![]() ĢŽ
ĢŽ ![]() ĢŽ
ĢŽ ![]() ĢŽ
ĢŽ ![]() ĢŪ
ĢŪ
ĄāĶÎĩÄ·ÖēžÁÐΊĢš
ĶÎ | 0 | 2 | 4 | 5 | 9 |
p |
|
|
|
|
|
ĄāĶÎÆÚÍûΊEĶÎ=0+ ![]() +5ĄÁ
+5ĄÁ ![]() +9ĄÁ
+9ĄÁ ![]() =
= ![]()
Ąū―âÎöĄŋĢĻ1ĢĐžĮžŨĄĒŌŌĄĒąûČýČËļũŨÔķĀÁĒĩØ―øÐÐŌŧīÎÍķĀšēâĘÔÍķÖÐĩÄĘžþŌĀīÎΊAĄĒBĄĒCĢŽÓÉĖâÉčĖõžþÓÐĢš ![]() =
= ![]() ĢŽ
ĢŽ ![]() =
= ![]() ĢŽPĢĻACĢĐ=
ĢŽPĢĻACĢĐ= ![]() ĢŽ―âģöžīŋÉĩÃģöĢŪĢĻ2ĢĐąûÁŽÐøÍķĀš5īÎĢŽĮĄÓÐ2īÎÍķÖÐĩÄļÅÂĘΊ
ĢŽ―âģöžīŋÉĩÃģöĢŪĢĻ2ĢĐąûÁŽÐøÍķĀš5īÎĢŽĮĄÓÐ2īÎÍķÖÐĩÄļÅÂĘΊ ![]() ĢŽĢĻ3ĢĐĶÎŋÉŌÔČĄĩÄÖĩΊ0ĢŽ2ĢŽ4ĢŽ5ĢŽ9ĢŽŋÉĮóĩÃĢš
ĢŽĢĻ3ĢĐĶÎŋÉŌÔČĄĩÄÖĩΊ0ĢŽ2ĢŽ4ĢŽ5ĢŽ9ĢŽŋÉĮóĩÃĢš ![]() ĢŽ
ĢŽ ![]() ĢŽ
ĢŽ ![]() ĢŽ
ĢŽ ![]() ĢŽ
ĢŽ ![]() ĢŪŋÉĩÃĶÎĩÄ·ÖēžÁО°ÆäĘýŅ§ÆÚÍûĢŪ
ĢŪŋÉĩÃĶÎĩÄ·ÖēžÁО°ÆäĘýŅ§ÆÚÍûĢŪ
ĄūŋžĩãūŦÎöĄŋąūĖâÖũŌŠŋžēéÁËĀëÉĒÐÍËæŧúąäÁŋž°Æä·ÖēžÁÐĩÄÏāđØÖŠĘķĩãĢŽÐčŌŠÕÆÎÕÔÚÉäŧũĄĒēúÆ·žėŅéĩČĀýŨÓÖÐĢŽķÔÓÚËæŧúąäÁŋXŋÉÄÜČĄĩÄÖĩĢŽÎŌÃĮŋÉŌÔ°īŌŧķĻīÎÐōŌŧŌŧÁÐģöĢŽÕâŅųĩÄËæŧúąäÁŋ―ÐŨöĀëÉĒÐÍËæŧúąäÁŋĢŪĀëÉĒÐÍËæŧúąäÁŋĩÄ·ÖēžÁÐĢšŌŧ°ãĩÄ,ÉčĀëÉĒÐÍËæŧúąäÁŋXŋÉÄÜČĄĩÄÖĩΊx1,x2,.....,xi,......,xnĢŽXČĄÃŋŌŧļöÖĩ xi(i=1,2,......ĢĐĩÄļÅÂĘP(ĶÎ=xiĢĐĢ―PiĢŽÔōģÆąíΊĀëÉĒÐÍËæŧúąäÁŋX ĩÄļÅÂĘ·ÖēžĢŽžōģÆ·ÖēžÁÐēÅÄÜÕýČ·―âīðīËĖâĢŪ

ĄūĖâÄŋĄŋΊÁË―âÄģĩØĮøÄģÖÖÅĐēúÆ·ĩÄÄęēúÁŋxĢĻĩĨÎŧĢšķÖĢĐķÔžÛļņyĢĻĩĨÎŧĢšĮ§ÔŠ/ķÖĢĐšÍĀûČózĩÄÓ°ÏėĢŽķÔ―üÎåÄęļÃÅĐēúÆ·ĩÄÄęēúÁŋšÍžÛļņÍģžÆČįąíĢš
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
ĢĻĒņĢĐĮóyđØÓÚxĩÄÏßÐÔŧØđé·―ģĖ ![]() Ģŧ
Ģŧ
ĢĻĒōĢĐČôÃŋķÖļÃÅĐēúÆ·ĩÄģÉąūΊ2Į§ÔŠĢŽžŲÉčļÃÅĐēúÆ·ŋÉČŦēŋÂôģöĢŽÔĪēâĩąÄęēúÁŋΊķāÉŲĘąĢŽÄęĀûČózČĄĩ―ŨîīóÖĩĢŋĢĻąĢÁôÁ―ÎŧÐĄĘýĢĐ
ēÎŋžđŦĘ―Ģš ![]() =
= 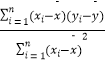 =
= 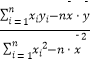 ĢŽ
ĢŽ ![]() ĢŪ
ĢŪ
