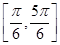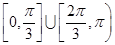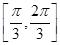题目内容
在直角坐标系xOy中,直线l的参数方程为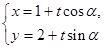 (t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位。且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位。且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为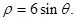
(I)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A,B.若点P的坐标为(1,2),求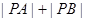 的最小值.
的最小值.
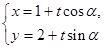 (t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位。且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位。且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为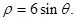
(I)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A,B.若点P的坐标为(1,2),求
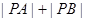 的最小值.
的最小值.(I)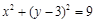 (Ⅱ)
(Ⅱ)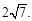
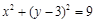 (Ⅱ)
(Ⅱ)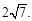
试题分析:由
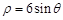 得
得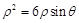 ,化为直角坐标方程为
,化为直角坐标方程为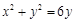 ,
,即
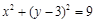 .
. (Ⅱ)将
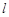 的参数方程代入圆C的直角坐标方程,得
的参数方程代入圆C的直角坐标方程,得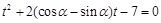 .
.由
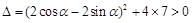 ,故可设
,故可设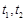 是上述方程的两根,
是上述方程的两根,所以
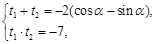 又直线
又直线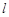 过点
过点 ,故结合t的几何意义得
,故结合t的几何意义得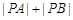 =
=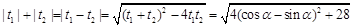

所以
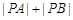 的最小值为
的最小值为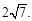
点评:本题主要考查曲线的参数方程与极坐标方程、直线的极坐标方程等基础知识,考查运算求解能力以及化归与转化思想、分类与整合思想,属于基础题.

练习册系列答案
相关题目
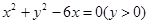 与直线
与直线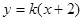 有公共点的充要条件是( )
有公共点的充要条件是( )



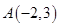 射出,经过
射出,经过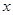 轴反射后,与圆
轴反射后,与圆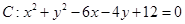 相切,则反射光线所在直线的方程为 .
相切,则反射光线所在直线的方程为 .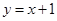 上的一点向圆
上的一点向圆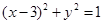 引切线,则切线长的最小值为
引切线,则切线长的最小值为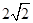
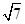
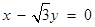 截圆
截圆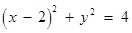 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是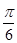



 ,若直线
,若直线 平分圆
平分圆 的周长,则
的周长,则 的最小值为
的最小值为 


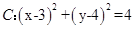 ,若直线
,若直线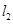 的方程为
的方程为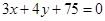 ,判断直线
,判断直线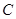 的位置关系;(2)若直线
的位置关系;(2)若直线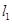 过定点
过定点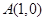 ,且与圆
,且与圆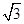 ,则直线倾斜角的取值范围是( )
,则直线倾斜角的取值范围是( )