题目内容

已知曲线C1：
x=2cosθ
y=2sinθ
（θ为参数），曲线C2=
x=1+tcosα
y=-1+tsinα
（t为参数）．
（1）若α=
π
4
，求曲线C2的普通方程，并说明它表示什么曲线；
（2）曲线C1和曲线C2的交点记为M，N，求|MN|的最小值．
分析：（1）将α的值代入曲线方程，消去参数t即可求出曲线C2的普通方程，再根据直线参数方程代表的几何意义可知；
（2）将弦长MN表示出来|MN|=2
4-|OG|2
，要使|MN|的最小值，只需弦心距最大即可，此时弦心距为OG，解之即可．
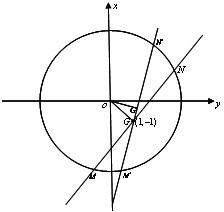解答：精英家教网解：（1）∵α=
π
4
∴
x=1+
2
2
t
y=-1+
2
2
t
（t为参数）
∴x-1=y+1，∴曲线C2的普通方程是y=x-2（2分）
它表示过（1，-1），倾斜角为
π
4
的直线（3分）
（2）曲线C1的普通方程为x2+y2=4（5分）
设G（1，-1），过G作MN⊥OG，
以下证明此时|MN|最小，
过G作直线M′N′，M′N′与MN不重合|M′N′|=2
4-|OG′|2
|MN|=2
4-|OG|2

在Rt△OG′G中，∵|OG|＞|OG′|∴|MN|＜|M′N′|（8分）
此时，|MN|=2
4-2
=2
2
（10分）
点评：本题主要考查了圆的参数方程、直线的参数方程，以及直线和圆的方程的应用，属于基础题．
练习册系列答案
相关题目
已知曲线C1：
x=3+2cosθ
y=2+2sinθ
(θ为参数)，曲线C2：
x=1+3t
y=1-4t
（t为参数），则C1与C2的位置关系为
 
．
（2012•云南模拟）已知曲线C1：
x=cosθ
y=sinθ
（θ为参数），曲线C2：
x=
2
2
t
y=
2
2
t-
2
（t为参数），
（1）曲线C1、C2是否有公共点，为什么？
（2）若把上各点的横坐标都压缩为原来的一半，分别得到曲线C1′、C2′，问C1′与C2′公共点的个数和C1与C2公共点的个数是否相同？说明你的理由．
已知曲线C1：
x=3+2cosθ
y=2+2sinθ
（θ为参数），曲线C2：
x=1+3t
y=1-4t
（t为参数），则C1与C2的位置关系为
相离
相离
．
[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
A．（选修4-1：几何证明选讲）
过圆O外一点P分别作圆的切线和割线交圆于A，B，且PB=7，∠ABP=∠ABC，C是圆上一点使得BC=5，求线段AB的长．
B．（选修4-2：矩阵与变换）
求曲线C：xy=1在矩阵
2
2
-
2
2
2
2
2
2
对应的变换作用下得到的曲线C′的方程．
C．（选修4-4：坐标系与参数方程）
已知曲线C1：
x=3cosθ
y=2sinθ
（θ为参数）和曲线C2：ρsin（θ-
π
4
）=
2
．
（1）将两曲线方程分别化成普通方程；
（2）求两曲线的交点坐标．
D．（选修4-5：不等式选讲）
已知|x-a|＜
c
4
，|y-b|＜
c
6
，求证：|2x-3y-2a+3b|＜c．
已知曲线C1：
x=-2+cost
y=1+sint
 （t为参数），C2：
x=4cosθ
y=3sinθ
（q为参数）．
（Ⅰ）化C1，C2的方程为普通方程，并说明它们分别表示什么曲线；
（Ⅱ）过曲线C2的左顶点且倾斜角为
π
4
的直线l交曲绒C1于A，B两点，求|AB|．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网