题目内容
(2012•云南模拟)已知曲线C1:
(θ为参数),曲线C2:
(t为参数),
(1)曲线C1、C2是否有公共点,为什么?
(2)若把上各点的横坐标都压缩为原来的一半,分别得到曲线C1′、C2′,问C1′与C2′公共点的个数和C1与C2公共点的个数是否相同?说明你的理由.
|
|
(1)曲线C1、C2是否有公共点,为什么?
(2)若把上各点的横坐标都压缩为原来的一半,分别得到曲线C1′、C2′,问C1′与C2′公共点的个数和C1与C2公共点的个数是否相同?说明你的理由.
分析:(1)先利用公式sin2θ+cos2θ=1将参数θ消去,得到圆的直角坐标方程,利用消元法消去参数t得到直线的普通方程,再根据圆心到直线的距离与半径进行比较,从而得到C1与C2公共点的个数;
(2)求出压缩后的参数方程,再将参数方程化为普通方程,联立直线方程与圆的方程,利用判别式进行判定即可.
(2)求出压缩后的参数方程,再将参数方程化为普通方程,联立直线方程与圆的方程,利用判别式进行判定即可.
解答:解:(1)C1的普通方程为x2+y2=1,圆心C1(0,0),半径r=1.…(1分)C2的普通方程为x-y-
=0.…(2分)
因为圆心C1到直线x-y-
=0的距离为1,…(4分)
所以C2与C1只有一个公共点.…(5分)
(2)压缩后的参数方程分别为C1′:
(θ为参数); C2′:
…(6分)
化为普通方程为:C1′:4x2+y2=1,C2′:y=2x-
,…(8分)
联立消元得8x2-4
x+1=0,其判别式△=(-4
)2-4×8×1=0,…(9分)
所以压缩后的直线C2′与椭圆C1′仍然只有一个公共点,和C1与C2公共点个数相同.…(10分)
| 2 |
因为圆心C1到直线x-y-
| 2 |
所以C2与C1只有一个公共点.…(5分)
(2)压缩后的参数方程分别为C1′:
|
|
化为普通方程为:C1′:4x2+y2=1,C2′:y=2x-
| 2 |
联立消元得8x2-4
| 2 |
| 2 |
所以压缩后的直线C2′与椭圆C1′仍然只有一个公共点,和C1与C2公共点个数相同.…(10分)
点评:本题主要考查了圆与直线的参数方程,以及直线圆的位置关系的判定,同时考查了利用判别式进行判定两曲线的公共点,转化与化归的思想方法,属于基础题.

练习册系列答案
相关题目
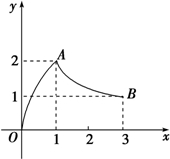 (2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(
(2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(