题目内容
8.已知A为曲线C:4x2-y+1=0上的动点,定点M(-2,0),若$\overrightarrow{AT}=2\overrightarrow{TM}$,求动点T的轨迹方程.分析 设出A(x0,y0),T(x,y),利用条件$\overrightarrow{AT}=2\overrightarrow{TM}$,到点A与点T坐标间的关系式,由此关系式代入点A所满足的方程y0=4x02+1,消去x0和y0,转化为x、y的方程.
解答 解:由题意,设A(x0,y0),T(x,y),
∵定点M(-2,0),$\overrightarrow{AT}=2\overrightarrow{TM}$,
∴(x-x0,y-y0)=2(-2-x,-y),
∴x0=3x+4,y0=3y,
∵A为曲线C:4x2-y+1=0上的动点,∴y0=4x02+1,
∴4(3x+4)2-3y+1=0,即为所求轨迹方程.
点评 本题的考点是圆锥曲线的轨迹问题,主要考查用代入法求轨迹方程,关键是理解题意,将向量条件转化为坐标关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.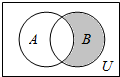 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )| A. | {3} | B. | {-2} | C. | {3,-2} | D. | {∅} |
16.已知△ABC的两边长分别为2,3,这两边的夹角的余弦值为$\frac{1}{3}$,则△ABC的外接圆的直径为( )
| A. | $\frac{9\sqrt{2}}{2}$ | B. | $\frac{9\sqrt{2}}{4}$ | C. | $\frac{9\sqrt{2}}{6}$ | D. | 8$\sqrt{2}$ |
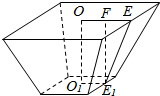 已知正四棱台高是12cm,两底面边长之差为10cm,全面积为512cm2.
已知正四棱台高是12cm,两底面边长之差为10cm,全面积为512cm2.