题目内容
设:P:指数函数y=ax在R内单调递减;Q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果P∨Q为真,¬Q也为真,求a的取值范围.
∵当0<a<1时,指数函数y=ax在R内单调递减,
当a>1时,指数函数y=ax在R内单调递增,
∴当命题P是真命题时,0<a<1;
当命题P是假命题时,a>1.
∵曲线y=x2+(2a-3)x+1与x轴有两个不同的交点等价于(2a-3)2-4>0,
解得a<
或a>
.
∴当命题Q是真命题时,则a<
或a>
;
当命题Q是假命题时,
≤a≤
.
∵P∨Q为真,¬Q也为真,
∴命题P是真命题,即0<a<1;
命题Q是假命题,即
≤a≤
,
因此,a∈(0,1)∩[
,
]=[
,1),
即a∈[
,1),
故a的取值范围是[
,1).
当a>1时,指数函数y=ax在R内单调递增,
∴当命题P是真命题时,0<a<1;
当命题P是假命题时,a>1.
∵曲线y=x2+(2a-3)x+1与x轴有两个不同的交点等价于(2a-3)2-4>0,
解得a<
| 1 |
| 2 |
| 5 |
| 2 |
∴当命题Q是真命题时,则a<
| 1 |
| 2 |
| 5 |
| 2 |
当命题Q是假命题时,
| 1 |
| 2 |
| 5 |
| 2 |
∵P∨Q为真,¬Q也为真,
∴命题P是真命题,即0<a<1;
命题Q是假命题,即
| 1 |
| 2 |
| 5 |
| 2 |
因此,a∈(0,1)∩[
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
即a∈[
| 1 |
| 2 |
故a的取值范围是[
| 1 |
| 2 |

练习册系列答案
相关题目


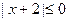 没有实数解”; (2)命题“-1是偶数或奇数”;
没有实数解”; (2)命题“-1是偶数或奇数”;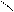 (3)命题“
(3)命题“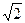 属于集合
属于集合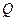 ,也属于集合
,也属于集合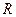 ”;(4)命题“
”;(4)命题“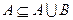 ”
”