题目内容
设命题p:|4x-3|≤1,命题q:x2-(2a+1)x+a(a+1)≤0,若“¬p⇒¬q”为假命题,“¬q⇒¬p”为真命题,求实数a的取值范围.
由|4x-3|≤1,得:-1≤4x-3≤1,解得:
≤x≤1,
因此,满足命题p的x的取值集合为{x|
≤x≤1},则满足命题¬p的x的取值集合为{x|x<
,或x>1};
由x2-(2a+1)x+a(a+1)≤0,得:(x-a)[x-(a+1)]≤0,解得:a≤x≤a+1.
因此,满足命题q的x的取值集合为{x|a≤x≤a+1},则满足命题¬q的x的取值集合为{x|x<a,或x>a+1};
由“¬p⇒¬q”为假命题,“¬q⇒¬p”为真命题,
得,{x|x<a,或x>a+1}⊆{x|x<
,或x>1}.
因此
,解得a∈[0,
].
所以,所求实数a的取值范围是[0,
].
| 1 |
| 2 |
因此,满足命题p的x的取值集合为{x|
| 1 |
| 2 |
| 1 |
| 2 |
由x2-(2a+1)x+a(a+1)≤0,得:(x-a)[x-(a+1)]≤0,解得:a≤x≤a+1.
因此,满足命题q的x的取值集合为{x|a≤x≤a+1},则满足命题¬q的x的取值集合为{x|x<a,或x>a+1};
由“¬p⇒¬q”为假命题,“¬q⇒¬p”为真命题,
得,{x|x<a,或x>a+1}⊆{x|x<
| 1 |
| 2 |
因此
|
| 1 |
| 2 |
所以,所求实数a的取值范围是[0,
| 1 |
| 2 |

练习册系列答案
相关题目
 是有理数
是有理数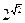 是实数
是实数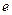 是有理数
是有理数

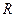
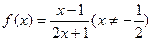 的对称中心是
的对称中心是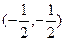 ;③对任意实数a,b则
;③对任意实数a,b则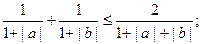 ④取一根长为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不少于1m的概率是
④取一根长为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不少于1m的概率是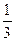 ;⑤如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则△A1B1C1为锐角三角形,△A2B2C2为钝角三角形.其中真命题的序号是 (将所有真命题的序号都填上).
;⑤如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则△A1B1C1为锐角三角形,△A2B2C2为钝角三角形.其中真命题的序号是 (将所有真命题的序号都填上).