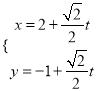题目内容
【题目】已知![]() ,函数
,函数![]() (
(![]() 是自然对数的底数).
是自然对数的底数).
(Ⅰ)若![]() ,证明:曲线
,证明:曲线![]() 没有经过点
没有经过点![]() 的切线;
的切线;
(Ⅱ)若函数![]() 在其定义域上不单调,求
在其定义域上不单调,求![]() 的取值范围;
的取值范围;
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)假设存在切线经过![]() ,设切点为
,设切点为![]() ,利用切线方程推出矛盾得到证明.
,利用切线方程推出矛盾得到证明.
(Ⅱ)函数![]() 在其定义域上不单调,等价于
在其定义域上不单调,等价于![]() 有变号零点,取导数为0,参数分离,设新函数利用函数的单调性求取值范围.
有变号零点,取导数为0,参数分离,设新函数利用函数的单调性求取值范围.
解:(Ⅰ)因为![]() ,所以
,所以![]() ,此时
,此时![]() ,
,
设曲线![]() 在点
在点![]() 处的切线经过点
处的切线经过点![]()
则曲线![]() 在点
在点![]() 处的切线
处的切线![]()
所以![]() 化简得:
化简得:![]()
令![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
当![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数,
所以![]() ,所以
,所以![]() 无解
无解
所以曲线![]() 的切线都不经过点
的切线都不经过点![]()
(Ⅱ)函数的定义域为![]() ,因为
,因为![]() ,
,
所以![]() 在定义域上不单调,等价于
在定义域上不单调,等价于![]() 有变号零点,
有变号零点,
令![]() ,得
,得![]() ,令
,令![]() .
.
因为![]() ,令
,令![]() ,
,![]() ,
,
所以![]() 是
是![]() 上的减函数,又
上的减函数,又![]() ,故1是
,故1是![]() 的唯一零点,
的唯一零点,
当![]() ,
,![]() ,
,![]() ,
,![]() 递增;
递增;
当![]() ,
,![]() ,
,![]() ,
,![]() 递减;
递减;
故当![]() 时,
时,![]() 取得极大值且为最大值
取得极大值且为最大值![]() ,所以
,所以![]() ,即
,即![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目
【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
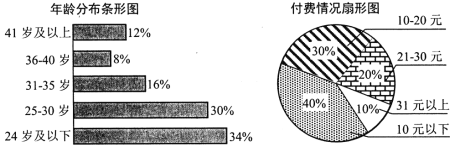
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
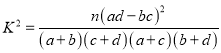 .
.