题目内容
关于非零平面向量 ,
, ,
, .有下列命题:
.有下列命题:①若
 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥b,则k=-3; ②若|
∥b,则k=-3; ②若| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°;
的夹角为60°;③|
 +
+ |=|
|=| |+|
|+| |?
|? 与
与 的方向相同; ④|
的方向相同; ④| |+|
|+| |>|
|>| -
- |?
|? 与
与 的夹角为锐角;
的夹角为锐角;⑤若
 =(1,-3),
=(1,-3), =(-2,4),
=(-2,4), =(4,-6),则表示向量4
=(4,-6),则表示向量4 ,3
,3 -2
-2 ,
, 的有向线段首尾连接能构成三角形.
的有向线段首尾连接能构成三角形.其中真命题的序号是 (将所有真命题的序号都填上).
【答案】分析:通过向量平行计算k的值判断①的正误;利用向量的平行四边形法则判断②的正误;通过向量的模的求法.判断③的正误;利用向量的三角形法则判断④的正误;通过向量的共线判断⑤的正误.
解答:解:对于①若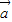 =(1,k),
=(1,k),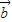 =(-2,6),
=(-2,6),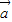 ∥b,所以-2k=6,所以k=-3,①正确;
∥b,所以-2k=6,所以k=-3,①正确;
对于②若|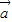 |=|
|=|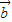 |=|
|=|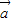 -
-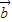 |,所以以|
|,所以以|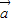 |,|
|,|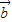 |,|
|,|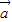 -
-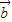 |,为三边的三角形是正三角形,则
|,为三边的三角形是正三角形,则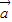 与
与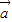 +
+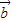 的夹角为30°,所以②不正确;
的夹角为30°,所以②不正确;
对于③|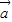 +
+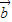 |=|
|=|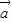 |+|
|+|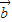 |?
|?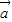 与
与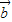 的方向相同;正确;
的方向相同;正确;
对于④|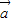 |+|
|+|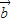 |>|
|>|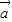 -
-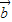 |?
|?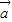 与
与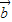 的夹角不为平角,所以④不正确;
的夹角不为平角,所以④不正确;
对于⑤若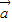 =(1,-3),
=(1,-3),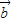 =(-2,4),
=(-2,4),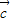 =(4,-6),则表示向量4
=(4,-6),则表示向量4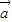 =(4,-12),3
=(4,-12),3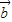 -2
-2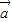 =(-8,18),
=(-8,18),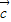 =(4,-6),因为3
=(4,-6),因为3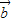 -2
-2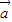 =-(4
=-(4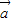 +
+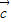 ),所以向量4
),所以向量4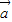 ,3
,3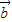 -2
-2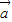 ,
,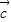 的有向线段首尾连接能构成三角形,不正确.
的有向线段首尾连接能构成三角形,不正确.
所以正确结果为①③.
故答案为:①③.
点评:本题考查命题的真假判断与应用,平面向量坐标表示的应用,向量的有关计算,考查计算能力.
解答:解:对于①若
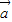 =(1,k),
=(1,k),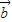 =(-2,6),
=(-2,6),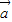 ∥b,所以-2k=6,所以k=-3,①正确;
∥b,所以-2k=6,所以k=-3,①正确;对于②若|
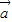 |=|
|=|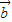 |=|
|=|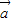 -
-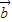 |,所以以|
|,所以以|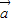 |,|
|,|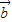 |,|
|,|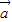 -
-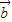 |,为三边的三角形是正三角形,则
|,为三边的三角形是正三角形,则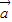 与
与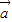 +
+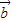 的夹角为30°,所以②不正确;
的夹角为30°,所以②不正确;对于③|
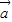 +
+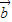 |=|
|=|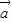 |+|
|+|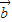 |?
|?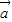 与
与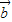 的方向相同;正确;
的方向相同;正确;对于④|
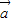 |+|
|+|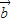 |>|
|>|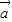 -
-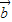 |?
|?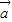 与
与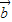 的夹角不为平角,所以④不正确;
的夹角不为平角,所以④不正确;对于⑤若
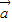 =(1,-3),
=(1,-3),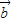 =(-2,4),
=(-2,4),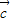 =(4,-6),则表示向量4
=(4,-6),则表示向量4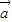 =(4,-12),3
=(4,-12),3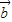 -2
-2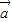 =(-8,18),
=(-8,18),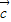 =(4,-6),因为3
=(4,-6),因为3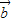 -2
-2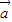 =-(4
=-(4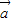 +
+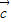 ),所以向量4
),所以向量4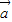 ,3
,3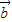 -2
-2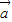 ,
,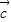 的有向线段首尾连接能构成三角形,不正确.
的有向线段首尾连接能构成三角形,不正确.所以正确结果为①③.
故答案为:①③.
点评:本题考查命题的真假判断与应用,平面向量坐标表示的应用,向量的有关计算,考查计算能力.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 ,
, ,
, .有下列命题:
.有下列命题: