题目内容
【题目】如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB= ![]() AD=2,点G为AC的中点.
AD=2,点G为AC的中点. 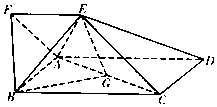
(Ⅰ)求证:平面BAE⊥平面DCE;
(Ⅱ)求三棱锥B﹣AEG的体积.
【答案】证明:(Ⅰ)∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴CD⊥平面AFED,∴CD⊥AE,
∵∠AED=90°,∴ED⊥AE,
又∵EO∩CD=D,∴AE⊥平面DCE,
又AE平面BAE,∴平面BAE⊥平面DCE.
(Ⅱ)作EN⊥AD,垂足为N,
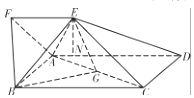
由平面ABCD⊥平面AFED,平面ABCD∩平面AFED=AD.
得EN⊥平面ABCD,即EN为三棱锥E﹣ABG的高.
∵在△AEF中,AF=FE,∠AFE=60°,∴△AEF是正三角形,AE=2,
由EF∥AD,知∠EAD=60°,∴ ![]() ,
,
∴三棱锥B﹣AEG的体积为:
![]() .
.
【解析】(Ⅰ)推导出CD⊥AE,ED⊥AE,从而AE⊥平面DCE,由此能证明平面BAE⊥平面DCE.(Ⅱ)作EN⊥AD,垂足为N,三棱锥B﹣AEG的体积为VB﹣AEG=VE﹣ABG,由此能求出结果.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

练习册系列答案
相关题目