题目内容
20.设函数y=f(x)的定义域是[0,4],则函数g(x)=$\frac{f(4x)}{lnx}$的定义域为(0,1).分析 由y=f(x)的定义域求出f(4x)的定义域,结合x>0且x≠1可得函数g(x)=$\frac{f(4x)}{lnx}$的定义域.
解答 解:∵y=f(x)的定义域是[0,4],由0≤4x≤4,得0≤x≤1.
∴f(4x)的定义域为[0,1],
又x>0且x≠1,
∴g(x)=$\frac{f(4x)}{lnx}$的定义域为(0,1).
故答案为:(0,1).
点评 本题考查函数的定义域及其求法,关键是求出f(4x)的定义域,是基础题.

练习册系列答案
相关题目
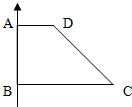 如图1,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,AD=2,AB=3,BC=6,把直角梯形ABCD绕边AB旋转一周得到一个旋转体,求:
如图1,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,AD=2,AB=3,BC=6,把直角梯形ABCD绕边AB旋转一周得到一个旋转体,求: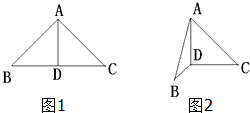 已知Rt△ABC中,AB=AC=a,AD是斜边BC上的高,以AD为折痕使∠BDC成直角,
已知Rt△ABC中,AB=AC=a,AD是斜边BC上的高,以AD为折痕使∠BDC成直角,