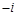题目内容
设数列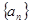 、
、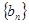 满足
满足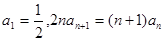 ,且
,且
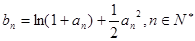 .
.
(1)求数列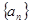 的通项公式;
的通项公式;
(2)对一切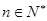 ,证明
,证明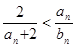 成立;
成立;
(3)记数列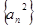 、
、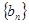 的前
的前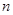 项和分别是
项和分别是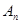 、
、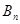 ,证明:
,证明: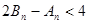 .
.
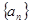 、
、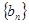 满足
满足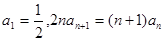 ,且
,且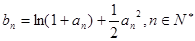 .
.(1)求数列
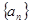 的通项公式;
的通项公式;(2)对一切
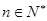 ,证明
,证明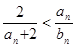 成立;
成立;(3)记数列
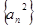 、
、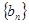 的前
的前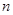 项和分别是
项和分别是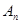 、
、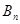 ,证明:
,证明: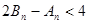 .
.(1)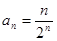 (2)略 (3)略
(2)略 (3)略
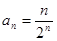 (2)略 (3)略
(2)略 (3)略本试题主要是考查了数列的递推关系的运用以及数列的求和问题的综合运用。
(1)先根据递推关系式变形得到数列的特点,分析概念得到通项公式。
(2)运用分析法结合函数的 思想得到不等式的证明。
(3)由于在上一问的基础上可知分析数列是等比数列的和,求和得到判定
(1)先根据递推关系式变形得到数列的特点,分析概念得到通项公式。
(2)运用分析法结合函数的 思想得到不等式的证明。
(3)由于在上一问的基础上可知分析数列是等比数列的和,求和得到判定

练习册系列答案
相关题目
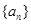 中,已知
中,已知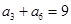 ,
, ,则
,则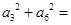
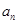 },
},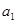 ·
·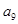 =16,则
=16,则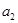 ·
·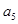 ·
·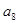 的值( )
的值( )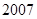 年
年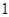 月
月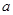 元,若按年利率为
元,若按年利率为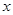 ,并按复利计算,到
,并按复利计算,到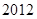 年
年 元
元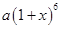 元
元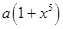 元
元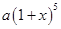 元
元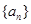 的前
的前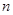 项和为
项和为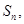 且
且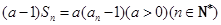 .
.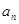 ;
;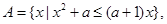 问是否存在实数
问是否存在实数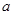 ,使得对于任意的
,使得对于任意的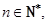 都有
都有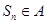 ? 若存在,求出
? 若存在,求出 项和为
项和为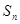 ,若
,若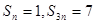 ,则
,则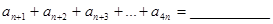
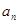 }满足
}满足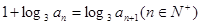 ,且
,且 ,则
,则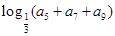 的值是 ( )
的值是 ( )

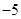
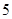
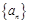 的通项公式为
的通项公式为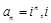 为虚数单位,则
为虚数单位,则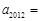 ( )
( )