题目内容
已知数列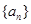 的前
的前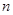 项和为
项和为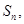 且
且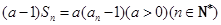 .
.
(1)求证数列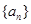 是等比数列,并求其通项公式
是等比数列,并求其通项公式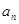 ;
;
(2)已知集合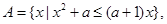 问是否存在实数
问是否存在实数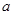 ,使得对于任意的
,使得对于任意的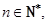 都有
都有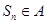 ? 若存在,求出
? 若存在,求出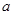 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
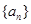 的前
的前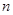 项和为
项和为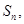 且
且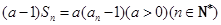 .
.(1)求证数列
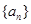 是等比数列,并求其通项公式
是等比数列,并求其通项公式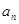 ;
;(2)已知集合
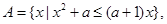 问是否存在实数
问是否存在实数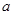 ,使得对于任意的
,使得对于任意的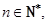 都有
都有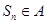 ? 若存在,求出
? 若存在,求出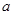 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.(1)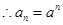 ;(2)
;(2) 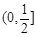 。
。
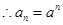 ;(2)
;(2) 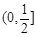 。
。(1)当n=1时可先求出a1.
当n>1时,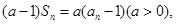
得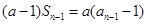
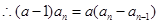 ,变形得
,变形得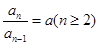
从而可得数列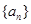 是等比数列,进而可求出其通项公式.
是等比数列,进而可求出其通项公式.
(2)要分a=1和a>1和0<a<1三种情况分别研究集合A,再研究是否满足题目条件.
(1)当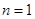 时,
时, 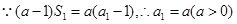
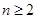 时,由
时,由
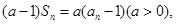 得
得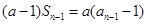
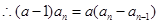 ,变形得
,变形得
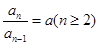 故
故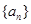 是以
是以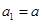 为首项,公比为
为首项,公比为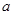 的等比数列,
的等比数列,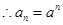 ---5分
---5分
(2)①当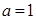 时,
时, 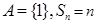 , 只有
, 只有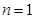 时,
时, , 所以
, 所以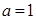 不合题意 ----7分
不合题意 ----7分
②当 时,
时, 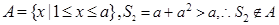 -----9分
-----9分
③当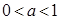 时,
时, 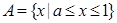 ,
,
而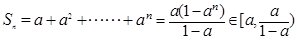 , 对任意
, 对任意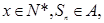

 综上,a的取值范围是
综上,a的取值范围是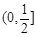 -------------12分
-------------12分
当n>1时,
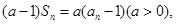
得
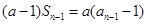
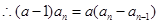 ,变形得
,变形得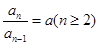
从而可得数列
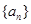 是等比数列,进而可求出其通项公式.
是等比数列,进而可求出其通项公式.(2)要分a=1和a>1和0<a<1三种情况分别研究集合A,再研究是否满足题目条件.
(1)当
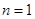 时,
时, 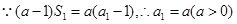
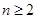 时,由
时,由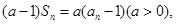 得
得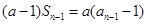
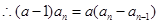 ,变形得
,变形得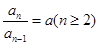 故
故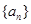 是以
是以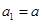 为首项,公比为
为首项,公比为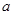 的等比数列,
的等比数列,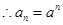 ---5分
---5分(2)①当
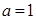 时,
时, 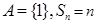 , 只有
, 只有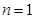 时,
时, , 所以
, 所以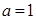 不合题意 ----7分
不合题意 ----7分②当
 时,
时, 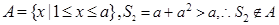 -----9分
-----9分③当
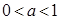 时,
时, 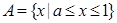 ,
, 而
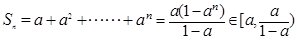 , 对任意
, 对任意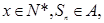

 综上,a的取值范围是
综上,a的取值范围是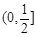 -------------12分
-------------12分
练习册系列答案
相关题目
 x
x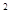 -
- x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.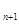 ;
;
 中,
中,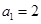 ,
,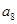 =4,函数
=4,函数 ,则
,则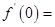 ( )
( )


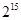
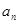 }的前n项和为
}的前n项和为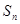 ,且
,且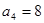 ,
, 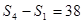 , 则数列{
, 则数列{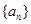 满足:
满足: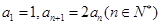 ,则
,则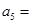 ;
;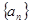 、
、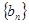 满足
满足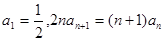 ,且
,且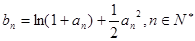 .
.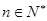 ,证明
,证明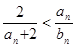 成立;
成立;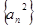 、
、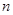 项和分别是
项和分别是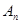 、
、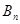 ,证明:
,证明: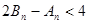 .
. 满足:
满足: 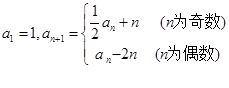
 ;
;  时,求
时,求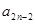 与
与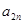 的关系式,并求数列
的关系式,并求数列