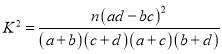题目内容
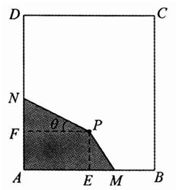
【题目】已知直线![]() 与椭圆
与椭圆![]() 相切于第一象限的点
相切于第一象限的点![]() ,且直线
,且直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,当
,当![]() (
(![]() 为坐标原点)的面积最小时,
为坐标原点)的面积最小时,![]() (
(![]() ,
,![]() 为椭圆的两个焦点),则此时
为椭圆的两个焦点),则此时![]() 中
中![]() 的平分线的长度为( )
的平分线的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
利用直线与椭圆相切可求得直线![]() 的方程为
的方程为![]() ,从而得到
,从而得到![]() ,结合基本不等式即可求出
,结合基本不等式即可求出![]() 面积最小时
面积最小时![]() 的取值情况,再利用余弦定理和面积公式即可求出结论.
的取值情况,再利用余弦定理和面积公式即可求出结论.
由题可知,直线![]() 的斜率一定存在,故可设直线
的斜率一定存在,故可设直线![]() 的方程为
的方程为![]() ,
,
联立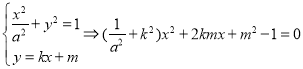 ,
,
又直线![]() 与椭圆相切,所以
与椭圆相切,所以![]() ,
,
即![]() ①,
①,
又直线![]() 过点
过点![]() ,即有
,即有![]() ②,
②,
且![]() 在椭圆上,即有
在椭圆上,即有![]() ③,
③,
由①②③可得![]() ,
,
因此直线![]() 的方程为
的方程为![]() ,
,
∴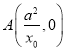 ,
,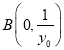 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
当且仅当![]() 时等号成立,此时
时等号成立,此时![]() 面积最小,
面积最小,
设![]() ,
,![]() ,则
,则![]() ,
,
由余弦定理,可知![]() ,
,
∴![]() ,
,![]() ,
,
又![]()
![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
设在![]() 中,
中,![]() 的平分线长度为
的平分线长度为![]() ,
,
则![]() ,
,
∴![]() ,
,
故选:B.

练习册系列答案
相关题目
【题目】为了研究广大市民对共享单车的使用情况,某公司在我市随机抽取了100名用户进行调查,得到如下数据:
每周使用次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
认为每周使用超过3次的用户为“喜欢骑共享单车”.
(1)分别估算男、女“喜欢骑共享单车”的概率;
(2)请完成下面的2×2列联表,并判断能否有95%把握,认为是否“喜欢骑共享单车”与性别有关.
不喜欢骑共享单车 | 喜欢骑共享单车 | 合计 | |
男 | |||
女 | |||
合计 |
附表及公式:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |