题目内容
设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为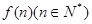
(1)求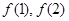 的值及
的值及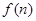 的表达式;
的表达式;
(2)设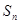 为数列
为数列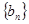 的前
的前 项的和,其中
项的和,其中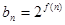 ,问是否存在正整数
,问是否存在正整数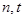 ,使
,使 成立?若存在,求出正整数
成立?若存在,求出正整数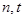 ;若不存在,说明理由
;若不存在,说明理由
(1)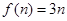 (2) 存在正整数
(2) 存在正整数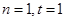 使
使 成立.
成立.
解析试题分析:(1)直接把n=1,2代入即可求出f(1),f(2)的值;再把x=1,x=2代入综合求出
f(n)的表达式;(2)先利用bn=2f(n)求出数列{bn}的通项公式,进而求出Sn;把Sn代入 ,化简得化简得,
,化简得化简得, (﹡),再分t=1以及t>1求出其对应的n即可说明结论.
(﹡),再分t=1以及t>1求出其对应的n即可说明结论.
⑴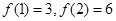
当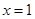 时,
时,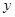 取值为1,2,3,…,
取值为1,2,3,…,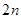 共有
共有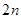 个格点
个格点
当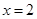 时,
时,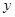 取值为1,2,3,…,
取值为1,2,3,…, 共有
共有 个格点
个格点
∴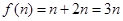
⑵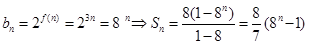
将 代入
代入 ,化简得,
,化简得, (﹡)
(﹡)
若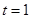 时
时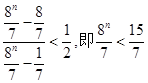 ,显然
,显然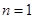
若 时
时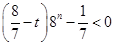 (﹡)式化简为
(﹡)式化简为 不可能成立
不可能成立
综上,存在正整数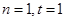 使
使 成立.
成立.
考点:数列与函数的综合;数列与不等式的综合.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
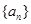 是公比为q的等比数列,其前n项的积为
是公比为q的等比数列,其前n项的积为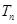 ,并且满足条件
,并且满足条件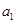 >1,
>1,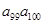 >1,
>1, 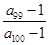 <0,给出下列结论:① 0<q<1;② T198<1;③
<0,给出下列结论:① 0<q<1;② T198<1;③ 的首项
的首项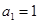 ,前
,前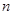 项和为
项和为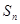 ,且
,且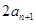 ,
,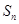 ,
,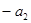 成等差数列,其中
成等差数列,其中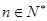 .
.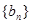 满足:
满足: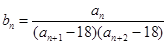 ,记数列
,记数列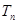 ,求
,求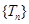 的最大项.
的最大项.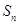 ,
,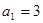 ,满足
,满足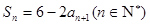 ,
,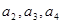 的值;
的值;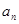 的表达式.
的表达式.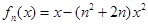 (其中
(其中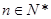 ),区间
),区间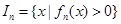 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为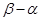 );
);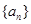 ,令
,令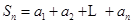 ,证明:
,证明: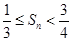 .
. 中,
中, ,且有
,且有 .
. 所有可能的值;
所有可能的值; ,都有
,都有 成立?若有,请写出这个数列的前6项,若没有,说明理由;
成立?若有,请写出这个数列的前6项,若没有,说明理由; 的最小值.
的最小值.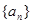 的首项
的首项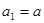 ,
,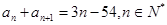
 项和为
项和为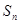 ,若
,若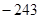 ,求
,求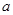 的取值范围?
的取值范围?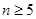 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: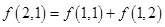 ;
;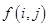 为数表中第
为数表中第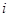 行的第
行的第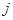 个数.
个数.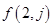 和
和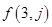 ;
;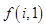 关于
关于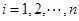 )的表达式.
)的表达式.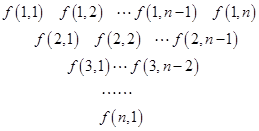
 ,
,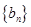 满足
满足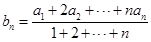
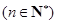 .
.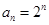 ,求数列
,求数列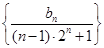 的前
的前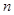 项和
项和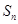 .
.