题目内容
已知向量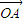
=（2，2），
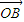=（4，1），在x轴上一点P，使
•
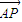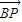有最小值，则P点的坐标是 ．
【答案】分析：设P（x，0），利用两个向量的数量积化简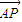
•
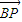的解析式，再利用二次函数的性质求出
•
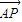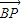最小时的x值，
从而得到P点的坐标．
解答：解析：设P（x，0），则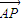
=（x-2，-2），
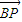=（x-4，-1）．
因此，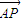
•
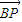=（x-4）（x-2）+2=x2-6x+10=（x-3）2+1．
∴当x=3时，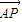
•
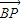取得最小值1，此时P（3，0），
故答案为：（3，0）．
点评：本题考查两个向量的数量积的运算，利用二次函数的性质求函数的最小值，属于中档题．
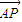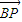• 的解析式，再利用二次函数的性质求出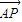• 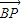最小时的x值，从而得到P点的坐标．
解答：解析：设P（x，0），则
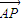=（x-2，-2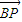），=（x-4，-1）．因此，
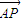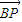•=（x-4）（x-2）+2=x2-6x+10=（x-3）2+1．∴当x=3时，
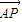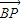•取得最小值1，此时P（3，0），故答案为：（3，0）．
点评：本题考查两个向量的数量积的运算，利用二次函数的性质求函数的最小值，属于中档题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知向量
=（-x，1），
=（x，tx），若函数f（x）=
•
在区间[-1，1]上不是单调函数，则实数t的取值范围是（ ）
| a |
| b |
| a |
| b |
| A、（-∞，-2]∪[2，+∞） |
| B、（-∞，-2）∪（2，+∞） |
| C、（-2，2） |
| D、[-2，2] |