题目内容
【题目】已知函数f(x)=lg( ![]() )为奇函数.
)为奇函数.
(1)求m的值,并求f(x)的定义域;
(2)判断函数f(x)的单调性,并证明;
(3)若对于任意θ∈[0, ![]() ],是否存在实数λ,使得不等式f(cos2θ+λsinθ﹣
],是否存在实数λ,使得不等式f(cos2θ+λsinθ﹣ ![]() )﹣lg3>0.若存在,求出实数λ的取值范围;若不存在,请说明理由.
)﹣lg3>0.若存在,求出实数λ的取值范围;若不存在,请说明理由.
【答案】
(1)解:∵函数f(x)=lg( ![]() )为奇函数,
)为奇函数,
∴f(﹣x)=﹣f(x)在定义域内恒成立,
即lg( ![]() )=﹣lg(
)=﹣lg( ![]() ),
),
即lg( ![]() )+lg(
)+lg( ![]() )=0,
)=0,
则 ![]()
![]() =1,即1﹣m2x2=1﹣x2,在定义域内恒成立,
=1,即1﹣m2x2=1﹣x2,在定义域内恒成立,
∴m=﹣1或m=1,当m=1时,f(x)=lg( ![]() )=lg1=0,
)=lg1=0,
∴m=﹣1,此时f(x)=lg ![]() ,
,
由 ![]() >0,解得﹣1<x<1,
>0,解得﹣1<x<1,
故函数的定义域是(﹣1,1)
(2)解:∵f(x)=lg ![]() ,﹣1<x<1,任取﹣1<x1<x2<1,
,﹣1<x<1,任取﹣1<x1<x2<1,
设u(x)= ![]() ,﹣1<x<1,
,﹣1<x<1,
则u(x1)﹣u(x2)= ![]()
∵﹣1<x1<x2<1,∴u(x1)﹣u(x2)<0,∴u(x1)<u(x2),即lgu(x1)<lgu(x2),
∴f(x1)<f(x2),即f(x)在定义域内单调递增
(3)解:假设存在实数λ,使得不等式不等式f(cos2θ+λsinθ﹣ ![]() )﹣lg3>0成立,
)﹣lg3>0成立,
即不等式f(cos2θ+λsinθ﹣ ![]() )>lg3=f(
)>lg3=f( ![]() ),
),
由(1),(2)知: ![]() <cos2θ+λsinθ﹣
<cos2θ+λsinθ﹣ ![]() <1 对于任意θ∈[0,
<1 对于任意θ∈[0, ![]() ],
],
即 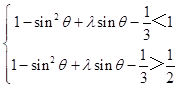 ,当θ=0时成立;
,当θ=0时成立;
当θ∈(0, ![]() ]时,令sinθ=t,则
]时,令sinθ=t,则  ,
,
即  ,则
,则 ![]()
【解析】(1)根据函数奇偶性的条件建立方程关系,即可求m的值,(2)根据函数单调性的定义即可判断函数f(x)的单调性;(3)利用三角函数姜不等式进行转化,解三角不等式即可得到结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案