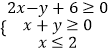题目内容
【题目】已知函数f（x）=loga（x﹣1），g（x）=loga（6﹣2x）（a＞0且a≠1）．
（1）求函数φ（x）=f（x）+g（x）的定义域；
（2）试确定不等式f（x）≤g（x）中x的取值范围．
【答案】
（1）解：由 
，解得1＜x＜3．
∴函数（x）的定义域为{x|1＜x＜3}
（2）解：不等式f（x）≤g（x），即为loga（x﹣1）≤loga（6﹣2x），
②当a＞1时，不等式等价于 
，解得： 
；
②当0＜a＜1时，不等式等价于 
，解得： 
．
综上可得，当a＞1时，不等式的解集为（1， 
]；
当0＜a＜1，不等式的解集为[ 
）
【解析】（1）直接由对数式的真数大于0联立不等式组求解x的取值集合得答案；（2）分a＞1和0＜a＜1求解不等式得答案．
【考点精析】本题主要考查了函数的定义域及其求法和指、对数不等式的解法的相关知识点，需要掌握求函数的定义域时，一般遵循以下原则：①
是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零；指数不等式的解法规律：根据指数函数的性质转化;对数不等式的解法规律：根据对数函数的性质转化才能正确解答此题．
练习册系列答案
相关题目
