题目内容
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,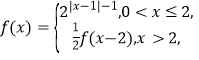 则函数
则函数![]() =
=![]() 在
在![]() 上的所有零点之和为
上的所有零点之和为
A. 7 B. 8 C. 9 D. 10
【答案】B
【解析】
试题∵函数f(x)是定义在R上的奇函数,∴f(-x)=-f(x).又∵函数g(x)=xf(x)-1,∴g(-x)=(-x)f(-x)-1=(-x)[-f(x)]-1=xf(x)-1=g(x),∴函数g(x)是偶函数,∴函数g(x)的零点都是以相反数的形式成对出现的.∴函数g(x)在[-6,6]上所有的零点的和为0,∴函数g(x)在[-6,+∞)上所有的零点的和,即函数g(x)在(6,+∞)上所有的零点之和.由0<x≤2时,f(x)=2|x-1|-1,即![]() ,∴函数f(x)在(0,2]上的值域为[
,∴函数f(x)在(0,2]上的值域为[![]() ,1],当且仅当x=2时,f(x)=1,又∵当x>2时,f(x)=
,1],当且仅当x=2时,f(x)=1,又∵当x>2时,f(x)=![]() f(x-2),∴函数f(x)在(2,4]上的值域为[
f(x-2),∴函数f(x)在(2,4]上的值域为[![]() ],函数f(x)在(4,6]上的值域为[
],函数f(x)在(4,6]上的值域为[![]() ],函数f(x)在(6,8]上的值域为[
],函数f(x)在(6,8]上的值域为[![]() ],当且仅当x=8时,f(x)=
],当且仅当x=8时,f(x)=![]() ,函数f(x)在(8,10]上的值域为[
,函数f(x)在(8,10]上的值域为[![]() ],当且仅当x=10时,f(x)=
],当且仅当x=10时,f(x)=![]() ,故f(x)<
,故f(x)<![]() 在(8,10]上恒成立,g(x)=xf(x)-1在(8,10]上无零点,同理g(x)=xf(x)-1在(10,12]上无零点,依此类推,函数g(x)在(8,+∞)无零点,综上函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为8,故选B
在(8,10]上恒成立,g(x)=xf(x)-1在(8,10]上无零点,同理g(x)=xf(x)-1在(10,12]上无零点,依此类推,函数g(x)在(8,+∞)无零点,综上函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为8,故选B

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案【题目】下表是![]() 年
年![]() 个重点城市(序号
个重点城市(序号![]() 为一线城市,其它为非一线城市)的月平均收入与房价对照表,根据表中数据并适当修正,得到房价中位数与月平均收入的线性回归方程是
为一线城市,其它为非一线城市)的月平均收入与房价对照表,根据表中数据并适当修正,得到房价中位数与月平均收入的线性回归方程是![]() ,我们把根据房价与月平均收入的线性回归方程得到的房价称为参考房价,若实际房价中位数大于参考房价,我们称这个城市是“房价偏贵城市”.
,我们把根据房价与月平均收入的线性回归方程得到的房价称为参考房价,若实际房价中位数大于参考房价,我们称这个城市是“房价偏贵城市”.
序号 | 月评价收入 | 房价中位数 | 参考房价 | 序号 | 月评价收入 | 房价中位数 | 参考房价 | 序号 | 月评价收入 | 房价中位数 | 参考房价 |
1 | 10670 | 67822 | 11 | 7081 | 17327 | 25704 | 21 | 7081 | 14792 | 15972 | |
2 | 10015 | 52584 | 51180 | 12 | 7065 | 13918 | 19476 | 22 | 7065 | 18741 | 15780 |
3 | 9561 | 50900 | 45732 | 13 | 7027 | 16286 | 19404 | 23 | 7027 | 10538 | 15324 |
4 | 8798 | 30729 | 36576 | 14 | 6974 | 16667 | 18204 | 24 | 6974 | 12069 | 14688 |
5 | 7424 | 10926 | 20088 | 15 | 6920 | 9743 | 17760 | 25 | 6920 | 2333 | 14040 |
6 | 7825 | 26714 | 24900 | 16 | 6903 | 10627 | 18120 | 26 | 6903 | 13582 | 13836 |
7 | 7770 | 39723 | 24240 | 17 | 6884 | 29000 | 17388 | 27 | 6884 | 22126 | 13608 |
8 | 7750 | 15114 | 24000 | 18 | 6654 | 7979 | 16584 | 28 | 6654 | 12207 | 10848 |
9 | 7723 | 17727 | 23676 | 19 | 6648 | 12500 | 16920 | 29 | 6648 | 12472 | 10776 |
10 | 7635 | 13012 | 22620 | 20 | 6608 | 12298 | 16200 | 30 | 6608 | 16406 | 10286 |
(1)计算城市![]() 的参考房价;
的参考房价;
(2)从![]() 个一线城市中随机选取
个一线城市中随机选取![]() 个城市进行调研,求恰好选到一个“房价偏贵城市”的概率;
个城市进行调研,求恰好选到一个“房价偏贵城市”的概率;
(3)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为一线城市与该城市为“房价偏贵城市”有关?
的把握认为一线城市与该城市为“房价偏贵城市”有关?
一般城市 | 非一线城市 | 总计 | |
房价偏贵城市 | |||
不是房价偏贵城市 | |||
总计 |
附参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.01 |
| 2.706 | 3.841 | 6.635 |