题目内容
1.已知x,y满足约束条件$\left\{\begin{array}{l}x-y-1≤0\\ 2x-y-3≥0\end{array}\right.$,当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值$2\sqrt{5}$时,ab的最大值为$\frac{5}{2}$.分析 由约束条件作出可行域,花目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得到$2a+b=2\sqrt{5}$,
然后利用基本不等式求得ab的最大值.
解答 解:由约束条件$\left\{\begin{array}{l}x-y-1≤0\\ 2x-y-3≥0\end{array}\right.$作出可行域如图,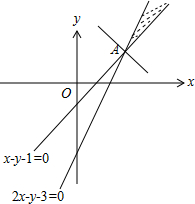
联立$\left\{\begin{array}{l}{x-y-1=0}\\{2x-y-3=0}\end{array}\right.$,解得A(2,1).
化目标函数z=ax+by(a>0,b>0)为$y=-\frac{a}{b}x+\frac{z}{b}$,
由图知在点(2,1)处取得最小值,则$2a+b=2\sqrt{5}$,
由基本不等式有:$2a+b=2\sqrt{5}≥2\sqrt{2ab}⇒ab≤\frac{5}{2}$.
∴ab的最大值为$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
18.设A,B,C三个集合,为使A?(B∪C),条件A?B是( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.已知等差数列{an}的公差d≠0,且a1≠d,记前20项之和S20=10M,则M=( )
| A. | a5+a6 | B. | a2+2a10 | C. | 2a10+d | D. | 10a2+d |
10.当|$\overrightarrow a$|=|$\overrightarrow b$|,且$\overrightarrow a$与$\overrightarrow b$不共线时,$\overrightarrow a$+$\overrightarrow b$与$\overrightarrow a$-$\overrightarrow b$的关系为( )
| A. | 平行 | B. | 垂直 | C. | 相交但不垂直 | D. | 相等 |
11.已知定义在R上的函数f(x)关于直线x=1对称,若x≥1时,f(x)=x(1-x),则f(0)=( )
| A. | 0 | B. | -2 | C. | -6 | D. | -12 |