题目内容
设x,y,z>0,x+y+z=3,依次证明下列不等式,
(1) (2-
(2- )≤1.
)≤1.
(2) ≥
≥ .
.
(3) +
+ +
+ ≥2.
≥2.
(1)
 (2-
(2- )≤1.
)≤1.(2)
 ≥
≥ .
.(3)
 +
+ +
+ ≥2.
≥2.见解析
证明:(1)由 (2-
(2- )=-[(
)=-[( )2-2
)2-2 +1]+1=-(
+1]+1=-( -1)2+1≤1,
-1)2+1≤1,
得 (2-
(2- )≤1.
)≤1.
当且仅当xy=1时取等号.
(2) ≥
≥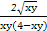
=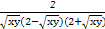 ,
,
因为2+ ≤2+
≤2+ ,且由(1)知
,且由(1)知 (2-
(2- )≤1,
)≤1,
当且仅当x=y=1时取等号.
所以 ≥
≥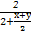 =
= ①.
①.
(3)同理可得 ≥
≥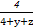 ②,
②,
 ≥
≥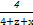 ③,
③,
由柯西不等式得( +
+ +
+ )(a+b+c)≥9,
)(a+b+c)≥9,
对于a,b,c>0, +
+ +
+ ≥
≥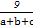 ④,
④,
利用不等式④,
由①,②,③及已知条件x + y + z =3得
 +
+ +
+ ≥
≥ +
+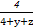 +
+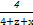 ≥
≥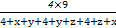 =
=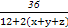 =2.
=2.
 (2-
(2- )=-[(
)=-[( )2-2
)2-2 +1]+1=-(
+1]+1=-( -1)2+1≤1,
-1)2+1≤1,得
 (2-
(2- )≤1.
)≤1.当且仅当xy=1时取等号.
(2)
 ≥
≥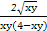
=
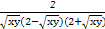 ,
,因为2+
 ≤2+
≤2+ ,且由(1)知
,且由(1)知 (2-
(2- )≤1,
)≤1,当且仅当x=y=1时取等号.
所以
 ≥
≥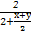 =
= ①.
①.(3)同理可得
 ≥
≥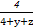 ②,
②, ≥
≥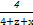 ③,
③,由柯西不等式得(
 +
+ +
+ )(a+b+c)≥9,
)(a+b+c)≥9,对于a,b,c>0,
 +
+ +
+ ≥
≥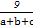 ④,
④,利用不等式④,
由①,②,③及已知条件x + y + z =3得
 +
+ +
+ ≥
≥ +
+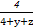 +
+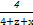 ≥
≥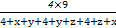 =
=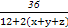 =2.
=2.
练习册系列答案
相关题目
 +
+ +
+ ≥a+b+c.
≥a+b+c. 的解集为(-1,4),则实数a的值为_________.
的解集为(-1,4),则实数a的值为_________. <0的解集是( )
<0的解集是( )
 ,3)
,3) >
> ;②ac<bc;③logb(a-c)>loga(b-c).
;②ac<bc;③logb(a-c)>loga(b-c). ,
, ,
, ,
, 中最大的是( )
中最大的是( )