题目内容
已知函数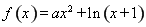 .
.
(1)当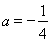 时,求函数
时,求函数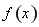 的单调区间;
的单调区间;
(2)若函数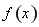 在区间
在区间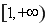 上为减函数,求实数
上为减函数,求实数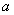 的取值范围;
的取值范围;
(3)当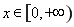 时,不等式
时,不等式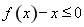 恒成立,求实数
恒成立,求实数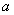 的取值范围.
的取值范围.
【答案】
(1)增区间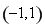 ,减区间
,减区间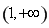 ;(2)
;(2) ;(3)
;(3)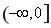 .
.
【解析】
试题分析:(1)将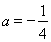 代入函数解析式,直接利用导数求出函数
代入函数解析式,直接利用导数求出函数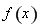 的单调递增区间和递减区间;(2)将条件“
的单调递增区间和递减区间;(2)将条件“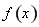 在区间
在区间 上为减函数”等价转化为“不等式
上为减函数”等价转化为“不等式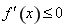 在区间
在区间 上恒成立”,结合参数分离法进行求解;(3)构造新函数
上恒成立”,结合参数分离法进行求解;(3)构造新函数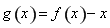 ,将“不等式
,将“不等式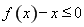 在区间
在区间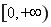 上恒成立”等价转化为“
上恒成立”等价转化为“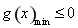 ”,利用导数结合函数单调性围绕
”,利用导数结合函数单调性围绕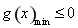 进行求解,从而求出实数
进行求解,从而求出实数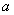 的取值范围.
的取值范围.
试题解析:(1)当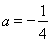 时,
时,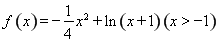 ,
,
 ,
,
解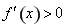 得
得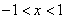 ;解
;解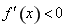 得
得 ,
,
故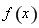 的单调递增区间是
的单调递增区间是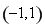 ,单调递减区间是
,单调递减区间是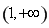 ;
;
(2)因为函数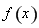 在区间
在区间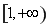 上为减函数,
上为减函数,
所以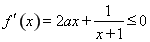 对
对 恒成立,
恒成立,
即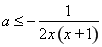 对
对 恒成立,
恒成立,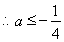 ;
;
(3)因为当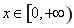 时,不等式
时,不等式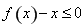 恒成立,
恒成立,
即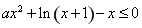 恒成立,设
恒成立,设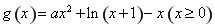 ,
,
只需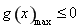 即可
即可
由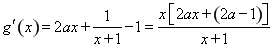 ,
,
①当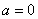 时,
时,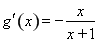 ,
,
当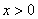 时,
时,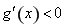 ,函数
,函数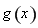 在
在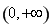 上单调递减,故
上单调递减,故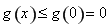 成立;
成立;
②当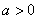 时,令
时,令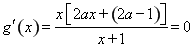 ,因为
,因为 ,所以解得
,所以解得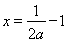 ,
,
(i)当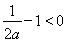 ,即
,即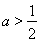 时,在区间
时,在区间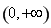 上
上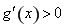 ,
,
则函数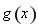 在
在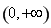 上单调递增,故
上单调递增,故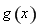 在
在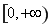 上无最大值,不合题设;
上无最大值,不合题设;
(ii)当 时,即
时,即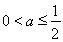 时,在区间
时,在区间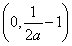 上
上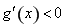 ;在区间
;在区间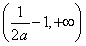 上
上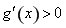 .
.
 函数
函数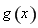 在
在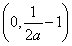 上单调递减,在区间
上单调递减,在区间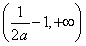 单调递增,同样
单调递增,同样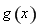 在
在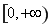 无最大值,不满足条件;
无最大值,不满足条件;
③当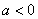 时,由
时,由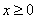 ,故
,故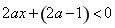 ,
,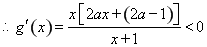 ,
,
故函数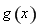 在
在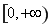 上单调递减,故
上单调递减,故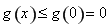 成立
成立
综上所述,实数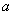 的取值范围是
的取值范围是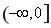 .
.
考点:1.函数的单调性与导数;2.分类讨论;3.参数分离法

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
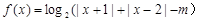 .
. 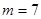 时,求函数
时,求函数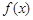 的定义域;
的定义域;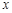 的不等式
的不等式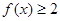 的解集是
的解集是 ,求
,求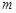 的取值范围.
的取值范围.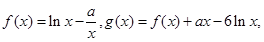
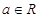 。
。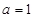 时,判断
时,判断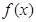 的单调性;
的单调性;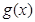 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数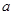 的取值范围;
的取值范围;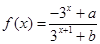 .
.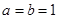 时,求满足
时,求满足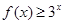 的
的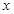 的取值范围;
的取值范围;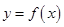 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求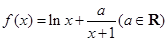 .
.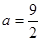 时,如果函数
时,如果函数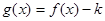 仅有一个零点,求实数
仅有一个零点,求实数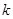 的取值范围;
的取值范围;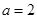 时,试比较
时,试比较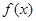 与
与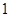 的大小;
的大小;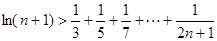 (
(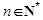 ).
).