题目内容
如图,在四棱锥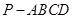 中,底面
中,底面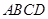 为直角梯形,且
为直角梯形,且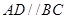 ,
,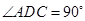 ,平面
,平面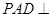 底面
底面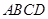 ,
,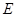 为
为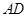 的中点,
的中点, 是棱
是棱 的中点,
的中点,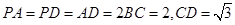 .
.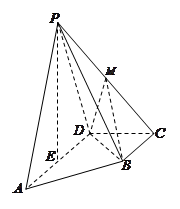
(1)求证: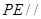 平面
平面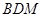 ;
;
(2)求三棱锥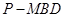 的体积.
的体积.
(1)见解析(2)
解析试题分析:(1)由题意知四边形BCDE为平行四边形,故连结CE交BD于O,知O是EC的中点,又M是PC的中点,根据中位线定理知MO∥PE,根据线面平行判定定理可得PE∥面BDM;(2)三棱锥P-MBD就是三棱锥P-BCD割去一个三棱锥M-BCD,故三棱锥P-MBD体积就是三棱锥P-BCD体积减去一个三棱锥M-BCD的体积,由PA=PD=AD=2及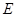 为
为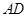 的中点知,PE垂直AD,由面面垂直的性质定理知PE⊥面ABCD,故PE是三棱锥P-BCD的高,由M是PC的中点知三棱锥M-BCD的高为PE的一半,故三棱锥P-MBD体积为三棱锥P-BCD体积的一半,易求出三棱锥P-BCD即可求出三棱锥P-MBD体积.
的中点知,PE垂直AD,由面面垂直的性质定理知PE⊥面ABCD,故PE是三棱锥P-BCD的高,由M是PC的中点知三棱锥M-BCD的高为PE的一半,故三棱锥P-MBD体积为三棱锥P-BCD体积的一半,易求出三棱锥P-BCD即可求出三棱锥P-MBD体积.
试题解析: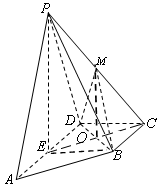
(1)连接 ,因为
,因为 ,
, ,所以四边形
,所以四边形 为平行四边形,
为平行四边形,
连接 交
交 于
于 ,连接
,连接 ,则
,则 ,
,
又 平面
平面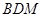 ,
, 平面
平面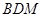 ,所以
,所以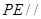 平面
平面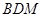 .
.
(2) ,
,
由于平面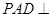 底面
底面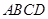 ,
,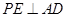
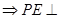 底面
底面
所以 是三棱锥
是三棱锥 的高,且
的高,且
由(1)知 是三棱锥
是三棱锥 的高,
的高, ,
,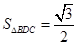 ,
,
所以 ,则
,则 .
.
考点:1.线面平行的判定;2.简单几何体体积计算;3.逻辑推理能力;4.空间想象能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 是边长为2的菱形,且
是边长为2的菱形,且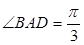 ,以
,以 与
与 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥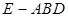 与
与 ,且
,且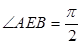 .
.
 平面
平面 的体积.
的体积. 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
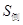 的值;
的值; 是半圆弧
是半圆弧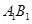 的中点,点
的中点,点 在半径
在半径 上,且
上,且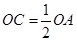 ,异面直线
,异面直线 与
与 所成的角为
所成的角为 ,求
,求 的值.
的值.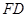 垂直于矩形
垂直于矩形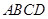 所在平面,
所在平面,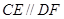 ,
, .
.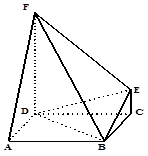
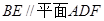 ;
; 的一个边
的一个边 ,
, ,则另一边
,则另一边 的长为何值时,三棱锥
的长为何值时,三棱锥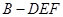 的体积为
的体积为 ?
?
 ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积. ,底面
,底面 是等腰梯形,且
是等腰梯形,且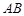 ∥
∥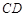 ,
, 是
是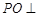 平面
平面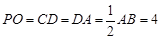 ,
, 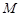 是
是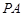 中点.
中点.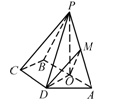
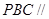 平面
平面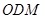 ;(2)求点
;(2)求点 到平面
到平面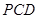 的距离.
的距离.
 为圆
为圆 的直径,点
的直径,点 .
.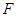 在圆
在圆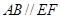 ,矩形
,矩形 所在的平面和圆
所在的平面和圆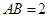 ,
,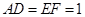 .
.
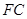 的中点为
的中点为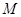 ,求证:
,求证: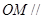 平面
平面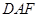 ;
;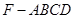 的体积.
的体积. ,则原四边形的面积是多少?
,则原四边形的面积是多少?