题目内容
如图,已知四棱锥 ,底面
,底面 是等腰梯形,且
是等腰梯形,且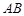 ∥
∥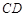 ,
, 是
是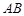 中点,
中点,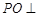 平面
平面 ,
,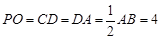 ,
, 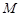 是
是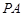 中点.
中点.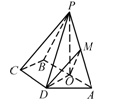
(1)证明:平面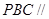 平面
平面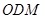 ;(2)求点
;(2)求点 到平面
到平面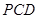 的距离.
的距离.
(1)详见解析;(2)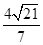
解析试题分析:(1)根据中位线可得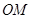 ∥
∥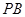 ,从而可证得
,从而可证得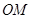 ∥平面
∥平面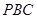 。证四边形
。证四边形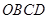 为平行四边形可得
为平行四边形可得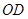 ∥平面
∥平面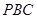 ,从而可证得平面
,从而可证得平面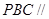 平面
平面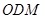 。(2)根据已知条件可得三棱锥
。(2)根据已知条件可得三棱锥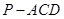 的体积,根据体积转化发即可求得点
的体积,根据体积转化发即可求得点 到平面
到平面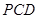 的距离。
的距离。
试题解析:(1) 证明:由题意,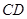 ∥
∥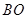 ,
,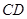 =
=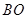
∴四边形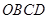 为平行四边形,所以
为平行四边形,所以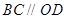 .
.
又∵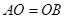 ,
,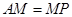 ∴
∴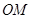 ∥
∥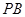
又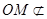 平面
平面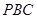 ,
,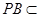 平面
平面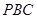 ∴
∴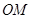 ∥平面
∥平面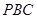 4分
4分
同理,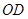 ∥平面
∥平面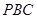 ,又
,又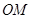
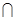
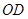
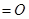
∴平面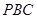 ∥平面
∥平面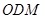 . 6分
. 6分
(2)设求点 到平面
到平面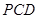 的距离为
的距离为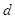 .
.
因为V三棱锥A-PCD= V三棱锥P-ACD即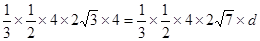
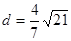 . 12分
. 12分
考点:1线线平行、线面平行;2点到面的距离。

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
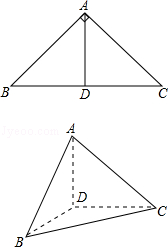
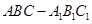 中,
中,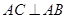 ,
, 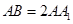 ,
,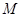 是
是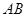 的中点,△
的中点,△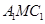 是等腰三角形,
是等腰三角形,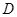 为
为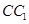 的中点,
的中点,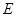 为
为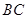 上一点.
上一点.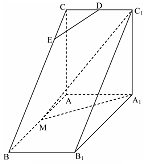
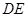 ∥平面
∥平面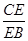 ;
;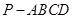 中,底面
中,底面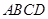 为直角梯形,且
为直角梯形,且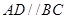 ,
,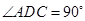 ,平面
,平面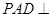 底面
底面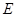 为
为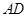 的中点,
的中点, 是棱
是棱 的中点,
的中点,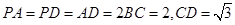 .
.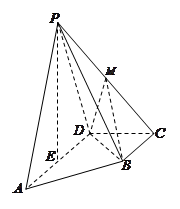
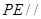 平面
平面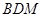 ;
;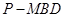 的体积.
的体积.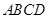 中,
中,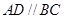 ,
,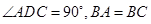 .把
.把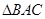 沿
沿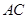 折起到
折起到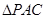 的位置,使得
的位置,使得 点在平面
点在平面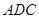 上的正投影
上的正投影 恰好落在线段
恰好落在线段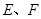 分别为棱
分别为棱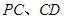 的中点.
的中点.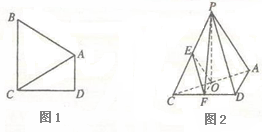
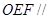 平面
平面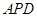 ;
;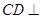 平面
平面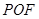 ;
; ,求四棱锥
,求四棱锥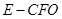 的体积.
的体积. A′B′C′,∠BAC=90°,AB=AC=
A′B′C′,∠BAC=90°,AB=AC= ,AA′=1,点M,N分别为
,AA′=1,点M,N分别为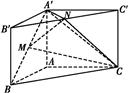
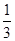 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高) 是边长为6的等边三角形,
是边长为6的等边三角形, 分别为
分别为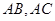 靠近
靠近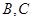 的三等分点,点
的三等分点,点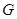 为边
为边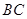 边的中点,线段
边的中点,线段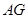 交线段
交线段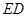 于点
于点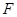 .将
.将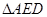 沿
沿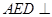 平面
平面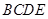 ,连接
,连接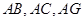 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.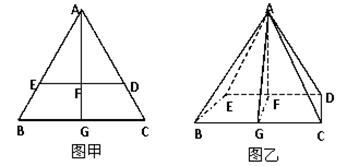
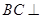 平面
平面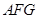
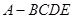 的体积.
的体积.  所在的平面和平面
所在的平面和平面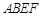 互相垂直,等腰梯形
互相垂直,等腰梯形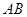 ∥
∥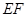 ,
,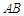 =2,
=2,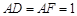 ,
,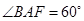 ,
,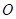 ,
, 分别为
分别为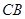 的中点,
的中点,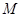 为底面
为底面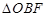 的重心.
的重心.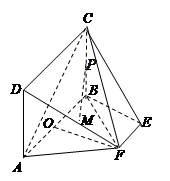
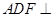 平面
平面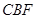 ;
;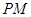 ∥平面
∥平面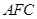 ;
; 的体积
的体积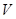 .
. 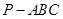 中,
中,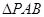 和
和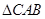 都是以
都是以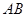 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,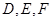 分别是
分别是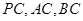 的中点.
的中点.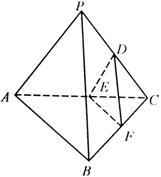
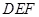 //平面
//平面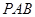 ;
;
 ;
;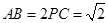 ,求三棱锥
,求三棱锥